粒子群算法介绍

粒子群算法（Particle Swarm Optimization，PSO）是一种受自然界鸟类飞行时集群的策略启发而得到的算法，其主要思想是利用种群中的每个个体进行探索，再将个体得到的最优解进行汇总比较，从而使得种群整体往全局最优解或者近似的方向去靠拢。

通俗来讲，可以将粒子看作是鸟，全局最优解代表栖息地或者食物，每个鸟抽象为质点，且都具有两个属性：速度和位置

注意：这里的速度是带有方向的，不是标量的速度

在最初的状态下，假设所有的鸟的速度和位置都是随机的，每个鸟都会向着自己的方向去进行探索。在下一轮更新中，每一只鸟都会向种群提交自己的位置信息，以及和栖息地或者食物的距离。

在完成一次搜索后，种群的鸟类会进行交流比对，并根据栖息地或者食物最可能存在的位置（种群最优解）去修正自己下一次的运动方向，但是不会完全改变自己的方向。同时，每一只鸟也会记录每一次自己离最优解的距离，并选取出最好的那次来修改自己的方向（个体最优解）

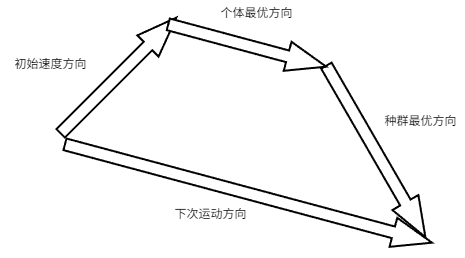
简单来说，就是鸟以最开始的方向为基础，根据个体最优解+种群最优解来不断修改自己的方向，并迭代自己的位置和速度参数，最后所有的鸟即整个种群会收敛到最优解的位置，如图所示

算法理论部分

以上的流程可以总结为下图的算法流程

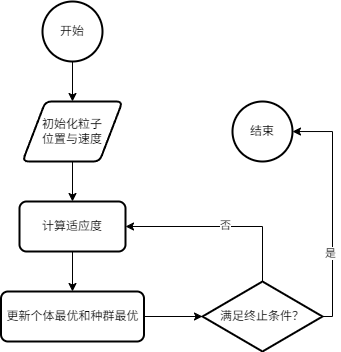
PSO算法的公式可以表示为

vi+1=ω×vi+c1×rand()×(pbest−xi)+c2×rand()×(gbest−xi)v_{i + 1} = \omega\times v_i + c_1\times rand()\times(p_{best} - x_i) + c_2\times rand()\times(g_{best} - x_i)

其中ω\omega为非负的惯性因子，viv_i为第ii次探索时的速度（i>1i > 1），c1c_1与c2c_2分别为超参数，rand()rand()为[0,1][0,1]上的随机数，pbestp_{best}为个体最优，gbestg_{best}为种群最优。

易知可以通过调整惯性因子来控制模型的全局搜索能力，当惯性因子较大时，全局搜索能力较强，但是收敛较慢，反之则全局搜索能力较弱，但是收敛速度快

可以理解为神经网络中的学习率，当学习率大时模型则会勇于学习新特征，当学习率低时则只会学习较为明显的特征

自然惯性因子也可以类似于神经网络中采用学习率衰减的情况，能够使用线性衰减来平衡全局搜索能力与收敛速度

ω(t)=(ωini−ωend)(Gk−g)/Gk+ωend\omega^{(t)} = (\omega_{ini} - \omega_{end})(G_k - g) / G_k + \omega_{end}

其中ωini\omega_{ini}为初始惯性因子，ωend\omega_{end}为终止惯性因子，GkG_k为模型最大迭代次数，gg为当前迭代次数

一般采用ωini=0.9\omega_{ini} = 0.9，ωend=0.4\omega_{end} = 0.4的参数

MATLAB代码实现

此处的适应度函数使用了Ackley函数

f(x)=−aexp⁡(−b1d∑i=1dxi2)exp⁡(1d∑i=1dcos⁡(cxi))+a+exp⁡(1)f(x)=-a\exp\left(-b\sqrt{\frac{1}{d}\sum_{i = 1}^dx_i^2}\right)\exp\left({\frac{1}{d}}\sum_{i=1}^d\cos(cx_i)\right)+a+\exp(1)

Ackley函数的MATLAB实现代码如下所示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
function value = Ackley_fun(x,dim)
    % Ackley函数
    % x为粒子的坐标
    % dim为空间的维度
    % 以下为建议的变量值
    a = 20;
    b = 0.2;
    c = 2 * pi;
    temp1 = 0;
    temp2 = 0;
    for iter = 1:dim
        temp1 = temp1 + x(iter) ^ 2;
        temp2 = temp2 + cos(c * x(iter));
    end
    value = -a * exp(-b * sqrt(temp1 / dim)) - exp(temp2 / dim) + a + exp(1);
end

为了使结果相对稳定，所以此处进行了多次实验取平均值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
clc,clear,clf
% 加速系数
c1 = 2;
c2 = 2;
iter_num = 20; % 迭代次数
total_num = 20; % 种群总数
dim = 2; % 维度
% 上下边界
p_max = 1;
p_min = 0;
% 速度上下限
V_max = 0.15 * p_max;
V_min = -V_max;
w_begin = 0.9; % 初始的惯性因子
w_end = 0.4; % 截止的惯性因子
mento_num = 100; % 蒙特卡洛仿真次数
% 第0代初始化
p_group = zeros(dim,total_num);
v_group = zeros(dim,total_num);
fitness = zeros(1,total_num);
for i = 1:total_num
    p_group(:,i) = p_max * rand(1,dim);
    v_group(:,i) = V_max * rand(1,dim);
    fitness(i) = Ackley_fun(p_group(:,i),dim); % Ackley为适应度评价函数
end
% 第0代种群寻优
[fitness_min,index_min] = min(fitness); % 第一代种群最佳适应度
P_best = p_group; % 个体历史最佳位置
G_best = p_group(:,index_min);% 全局历史最佳位置
fitness_best = fitness; % 个体历史最佳适应度
fitness_G_best = fitness_min; % 全局历史最佳适应度
result = zeros(mento_num,iter_num); % 历代全局历史最佳适应度
G_best_list = zeros(dim,mento_num); % 历代全局历史最佳位置

for j = 1:mento_num
    % 进行mento_num次实验
    for iter_time = 1:iter_num
        % 迭代每一代
        for k = 1:total_num
            % 更新每个粒子
            w = (w_begin - w_end) * (iter_num - iter_time) / iter_num + w_end;
            % 速度更新
            v_group(:,k) = w * v_group(:,k) + c1 * rand * (P_best(:,k) - p_group(:,k)) + c2 * rand * (G_best - p_group(:,k));
            % 速度越界处理
            v_group(v_group(:,k) > V_max,k) = V_max;
            v_group(v_group(:,k) < V_min,k) = V_min;
            % 位置更新
            p_group(:,k) = p_group(:,k) + v_group(:,k);
            % 位置越界处理
            p_group(p_group(:,k) > p_max,k) = p_max;
            p_group(p_group(:,k) < p_min,k) = p_min;
            % 计算适应度
            fitness(k) = Ackley_fun(p_group(:,i),dim);
            % 个体历史最优更新
            if fitness(k) < fitness_best(k)
                P_best(:,k) = p_group(:,k);
                fitness_best(k) = fitness(k);
            end
        end
        % 种群历史最优更新
        p_group_best = find(fitness_best < fitness_G_best);
        % 第iter代种群所有粒子最佳历史适应度与全局历史最佳适应度比较
        if isempty(p_group_best) == 0
            if length(p_group_best) ~= 1
                % 如果多个粒子历史最佳适应度都优于全局历史最佳适应度，随机挑选
                p_group_best = randsrc(1,1,p_group_best);
            end
            G_best = p_group(:,p_group_best); % 种群全局历史最佳位置更新
            fitness_G_best = fitness_best(p_group_best); % 种群全局历史最佳适应度更新
        end
        result(j,iter_time) = fitness_G_best;
    end
    G_best_list(:,j) = G_best;
end

[~,INDEX] = min(result(:,iter_num)); % 比较最后一次迭代的适应度
FITNESS_RESULT = mean(result);
G_best_result = G_best_list(:,INDEX);

plot(FITNESS_RESULT);
grid on;                
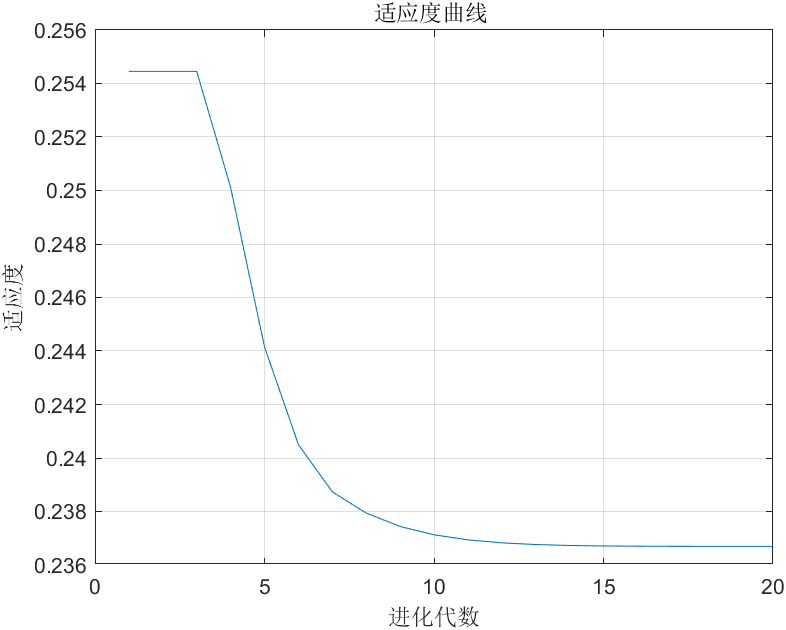
title('适应度曲线 ');
xlabel('进化代数')
ylabel('适应度');

最后可以得到结果