电磁场与波笔记

矢量分析

矢量代数

标量：只有大小，没有方向的量

矢量：既有大小，又有方向的量

对于矢量 $\pmb{A}$ ，我们常用 $\pmb e_A$ 表示与其同方向的单位矢量

矢量的加减运算遵循平行四边形定则，此处不做赘述

矢量的乘积运算有两种，点积和叉积

对于点积有

$\pmb A \cdot \pmb B = AB\cos\theta$

对于叉积有

$\pmb A \times \pmb B = \pmb e_nAB\sin\theta$

点积之后的结果是一个标量，而叉积之后的结果是一个矢量，其方向遵循右手螺旋定则

矢量的叉积运算一般使用行列式进行计算

$\pmb A\times\pmb B = \left| \begin{array}{cccc} \pmb e_x & \pmb e_y & \pmb e_z \\ A_x & A_y & A_z\\ B_x & B_y & B_z \end{array} \right|$

对于点积和叉积分别有标量三重积 $\pmb A \cdot (\pmb B \times \pmb C)$ 和矢量三重积 $\pmb A \times (\pmb B\times \pmb C)$

标量三重积有以下运算性质

$\pmb A \cdot (\pmb B \times \pmb C) = \pmb B \cdot (\pmb C \times \pmb A) = \pmb C \cdot(\pmb A\times\pmb B)$

矢量三重积有以下运算性质

$\pmb A\times (\pmb B\times \pmb C) = \pmb B(\pmb A\cdot \pmb C) - \pmb C(\pmb A\cdot \pmb B)$

三种常用的正交曲线坐标系

直角坐标系

比较熟悉，最常用的坐标系

三个坐标变量的变化范围是 $-\infty < x,y,z < \infty$

位置矢量是

$\pmb r = \pmb e_xx + \pmb e_yy + \pmb e_zz$

其微分为

$d\pmb r = \pmb e_xdx + \pmb e_ydy + \pmb e_zdz$

面元和体积元分别为

$dS_x = dydz,dS_y = dxdz,dS_z = dxdy$

$dV = dxdydz$

圆柱坐标系

三个坐标变量的变化范围是 $0\le \rho<\infty,0\le \phi\le 2\pi,-\infty< z< \infty$

与直角坐标系的变换关系为

$\rho = \sqrt{x^2 + y^2},\phi = \arctan(y/x),z=z$

或

$x = \rho\cos\phi,y = \rho\sin\phi,z=z$

位置矢量为

$\pmb r = \pmb e_\rho\rho + \pmb e_zz$

其微分元矢量为

$d\pmb r = \pmb e_\rho d\rho + \pmb e_\phi\rho d\phi + \pmb e_zdz$

面积元和体积元分别为

$dS_\rho = \rho d\phi dz,dS_\phi = d\rho dz,dS_z = \rho d\rho d\phi$

$dV = \rho d\rho d\phi dz$

球坐标系

三个坐标变量的取值范围是

$0\le r<\infty,0\le\theta\le\pi,0\le\phi\le2\pi$

与直角坐标系之间的变换关系

$r = \sqrt{x^2 + y^2 + z^2},\theta = \arccos(z/\sqrt{x^2 + y^2 + z^2}),\phi = \arctan(y/x)$

或

$x = r\sin\theta\cos\phi,y = r\sin\theta\sin\phi,z = r\cos\theta$

其位置矢量是

$\pmb r = \pmb e_rr$

微分元矢量为

$d\pmb r = \pmb e_rdr + \pmb e_\theta rd\theta + \pmb e_\phi r\sin\theta d\phi$

面积元和体积元分别为

$dS_r = r^2\sin\theta d\theta d\phi,dS_\theta = r\sin\theta drd\phi,dS_\phi = rdrd\theta$

$dV = r^2\sin\theta drd\theta d\phi$

标量场的方向导数和梯度

标量场

若我们研究的物理量是一个标量，则由其所确定的场称为标量场

一个标量场可以用一个标量函数来表示，即

$u = u(x,y,z,t)$

或者由位置矢量来表示

$u = u(\pmb r,t)$

对于和时间无关的标量场，则可以表示为

$u = u(\pmb r)$

对于任意给定的常数 $c$ ，方程 $u(\pmb r) = c$ 就是等值面方程

等值面方程具有以下特点

常数 $c$ 取不同的值，就可以得到不同的等值面，从而可形成等值面族
标量场的等值面族会充满场所在的整个空间
由于标量函数 $u(\pmb r)$ 是单值的，一个点只能在一个等值面上，所以等值面之间互不相交

方向导数

设 $M_0$ 是标量场 $u(M)$ 中的一点，从点 $M_0$ 出发引一条射线 $\pmb l$ ，点 $M$ 是射线 $\pmb l$ 上的动点，到点 $M_0$ 的距离为 $\Delta l$

当点 $M$ 沿射线 $\pmb l$ 趋近于 $M_0$ 时，比值 $\displaystyle\frac{u(M) - u(M_0)}{\Delta l}$ 的极限称为标量场 $u(M)$ 在点 $M_0$ 处沿 $\pmb l$ 方向的方向导数，即

$\frac{\partial u}{\partial l}|_{M_0} = \underset{\Delta l \rightarrow 0}{\lim}\frac{u(M) - u(M_0)}{\Delta l}$

方向导数的物理含义就是标量场 $u(M)$ 在点 $M_0$ 处沿 $\pmb l$ 方向的变化率

当 $\displaystyle\frac{\partial u}{\partial l} > 0$ 时，标量场 $u(M)$ 沿 $\pmb l$ 方向是增加的；反之则是减小的

如果 $\displaystyle\frac{\partial u}{\partial l} = 0$ ，则无变化

在直角坐标系当中，若射线 $\pmb l$ 与 $x,y,z$ 轴的夹角分别为 $\alpha,\beta,\gamma$ ，则有

$\frac{dx}{dl} = \cos\alpha,\frac{dy}{dl} = \cos\beta,\frac{dz}{dl} = \cos\gamma$

式子当中的 $\cos\alpha,\cos\beta,\cos\gamma$ 为 $\pmb l$ 的方向余弦，可得直角坐标系当中的方向导数的计算公式

$\frac{\partial u}{\partial l} = \frac{\partial u}{\partial x}\cos\alpha + \frac{\partial u}{\partial y}\cos\beta + \frac{\partial u}{\partial z}\cos\gamma$

梯度

在直角坐标系当中，梯度的具体表达式如下

$\mathbf{grad}\ u = \pmb e_x\frac{\partial u}{\partial x} + \pmb e_y\frac{\partial u}{\partial y} + \pmb e_z\frac{\partial u}{\partial z}$

此处我们定义 $\pmb \nabla$ 为哈密顿算符，在直角坐标系当中有

$\pmb \nabla = \pmb e_x\frac{\partial}{\partial x} + \pmb e_y\frac{\partial}{\partial y} + \pmb e_z\frac{\partial}{\partial z}$

所以则有

$\mathbf{grad} \ u = \pmb\nabla u$

在圆柱坐标系和球坐标系当中，梯度的计算公式为

$\pmb \nabla u = \pmb e_\rho\frac{\partial u}{\partial \rho} + \pmb e_\phi\frac{\partial u}{\rho\partial \phi} + \pmb e_z\frac{\partial u}{\partial z}$

$\pmb \nabla u = \pmb e_r\frac{\partial u}{\partial r} + \pmb e_\theta\frac{\partial u}{r\partial \theta} + \pmb e_\phi\frac{\partial u}{r\sin\theta\partial \phi}$

由以上分析可知，标量场的梯度有以下特点

通常称 $\pmb \nabla u$ 为标量场 $u$ 产生的梯度场
标量场 $u$ 在给定定点 $M$ 处沿任意方向 $\pmb e_l$ 的方向导数等于该点的梯度 $\pmb\nabla u$ 在方向 $\pmb e_l$ 上的投影
标量场 $u$ 在点 $M$ 处的梯度垂直于过该点的等值面，且指向 $u(M)$ 增加的方向

通量和散度

一个矢量场 $\pmb F$ 可以被分解为三个标量场，即 $\pmb F(x,y,z) = \pmb e_xF_x(x,y,z) + \pmb e_yF_y(x,y,z) + \pmb e_zF_z(x,y,z)$

对于矢量场 $\pmb F(r)$ ，可以用一些有向曲线来形象的描述矢量在空间的分布，即矢量线

设 $M$ 是矢量线上任意一点，位置矢量是 $\pmb r$ ，则其微分矢量 $d\pmb r$ 在点 $M$ 处与矢量线相切，即

$d\pmb r\times\pmb F = 0$

则可推出矢量线方程

$\frac{dx}{F_x} = \frac{dy}{F_y} = \frac{dz}{F_z}$

在矢量场 $\pmb F$ 当中，矢量穿过面元矢量的通量可定义为 $\pmb F\cdot d\pmb S$ ，将各个面元相加即可得到曲面 $S$ 的通量

$\Phi = \int_S\pmb F\cdot d\pmb S$

如果 $S$ 是一个闭合曲面，则可表示为

$\Phi = \oint_S\pmb F\cdot d\pmb S$

在矢量场 $\pmb F$ 中任意一点 $M$ 作一个包围该点的任意闭合曲面 $S$ ，当 $S$ 以任意方式收缩到点 $M$ 时，所限定的体积 $\Delta V$ 将趋于0

如果极限 $\displaystyle\frac{\oint_S\pmb F\cdot d\pmb S}{\Delta V}$ 存在，则将此极限称为矢量场 $\pmb F$ 在点 $M$ 处的散度，并记作 $div \ \pmb F$ ，即

$div \ \pmb F = \underset{\Delta V\rightarrow0}{\lim}\displaystyle\frac{\oint_S\pmb F\cdot d\pmb S}{\Delta V}$

$\begin{cases}div\ \pmb F > 0&\text{正通量源}\\\\div\ \pmb F < 0&\text{负通量源}\\\\div\ \pmb F = 0&\text{无通量源}\end{cases}$

散度定理

散度定理即高斯定理，它表明矢量场的散度在任意体积 $\pmb V$ 上的体积分等于矢量场穿出限定该体积的闭合曲面 $\pmb S$ 的通量，即

$\int_V\pmb\nabla\cdot\pmb FdV = \oint_S\pmb F\cdot d\pmb S$

矢量场的环流和旋度

环流和环流面密度

矢量场 $\pmb F$ 沿场中的一条有向闭合路径 $C$ 的曲线积分

$\Gamma = \oint_C\pmb F\cdot d\pmb l$

称为矢量场沿闭合路径 $C$ 的环流

对于矢量场当中任意一点 $M$ ，选取一个方向矢量 $\pmb e_n$ ，并且以其为法向矢量作一面元矢量 $\Delta S$ ，边界为有向闭合路径 $C$ ，若极限 $\displaystyle\underset{\Delta S\rightarrow 0}{\lim}\frac{\oint_C\pmb F\cdot d\pmb l}{\Delta S}$ 存在，则称该极限为矢量场在点 $M$ 处沿方向 $\pmb e_n$ 的环流面密度，记作 ${rot}_n\ \pmb F$ ，即

${rot}_n\ \pmb F = \underset{\Delta S\rightarrow 0}{\lim}\frac{\oint_C\pmb F\cdot d\pmb l}{\Delta S}$

由此定义可知，环流面密度不仅和点 $M$ 的位置有关，还和面元矢量的法向矢量有关

矢量场的旋度

矢量场 $\pmb F$ 在点 $M$ 处的旋度定义为一个矢量，以符号 $rot\ F$ 表示，它在点 $M$ 处沿方向 $\pmb e_n$ 的分量等于矢量场在点 $M$ 处沿方向 $\pmb e_n$ 的环流面密度，即

$\pmb e_n\cdot rot\ \pmb F = {rot}_n\ \pmb F$

易知当 $\pmb e_n$ 和 $rot\ \pmb F$ 的方向相同时， $\pmb e_n\cdot rot\ \pmb F$ 的值最大为 $|rot\ \pmb F|$

因此， $rot\ \pmb F$ 的方向是使矢量场在 $M$ 点处取得最大环流面密度的方向，其模值等于最大的环流面密度

直角坐标系，圆柱坐标系和球坐标系的旋度的计算公式分别为

$rot\ \pmb F = \pmb e_x\left({\frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z}}\right) + \pmb e_y\left({\frac{\partial F_x}{\partial z} - \frac{\partial F_z}{\partial x}}\right) + \pmb e_z\left({\frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y}}\right) = \pmb\nabla\times\pmb F$

$rot\ \pmb F = \pmb e_\rho\ \left({\frac{1}{\rho}\frac{\partial F_z}{\partial\phi} - \frac{\partial F_\phi}{\partial z}}\right) + \pmb e_\phi\ \left({\frac{\partial F_\rho}{\partial z} - \frac{\partial F_z}{\partial \rho}}\right) + \pmb e_z\ \frac{1}{\rho}\left[{\frac{\partial (\rho F_\phi)}{\partial\rho} - \frac{\partial F_\rho}{\partial \phi}}\right]$

$rot\ \pmb F = \pmb e_r\frac{1}{r\sin\theta}\left[{\frac{\partial}{\partial\theta}(\sin\theta F_\phi) - \frac{\partial F_\theta}{\partial\phi}}\right] + \pmb e_\theta\frac{1}{r}\left[{\frac{1}{\sin\theta}\frac{\partial F_r}{\partial\phi} - \frac{\partial (rF_\phi)}{\partial r}}\right] + \pmb e_\phi\frac{1}{r}\left[{\frac{\partial (rF_\theta)}{\partial r} - \frac{\partial F_r}{\partial\theta}}\right]$

斯托克斯定理

矢量场 $\pmb F$ 的旋度 $\pmb\nabla\times\pmb F$ 在曲面 $S$ 上的面积分等于矢量场在限定曲面的闭合曲线 $C$ 上的线积分，即

$\int_S\pmb\nabla\times\pmb F\cdot d\pmb S = \oint_C\pmb F\cdot d\pmb l$

无旋场的标量位

如果一个矢量场的旋度处处为0，即

$\pmb\nabla\times\pmb F \equiv 0$

则称该矢量场为无旋场，它是由散度源产生的

利用斯托克斯定理可知，无旋场沿闭合路径 $C$ 的环流等于0，也就是说，无旋场内的曲线积分与路径无关，只和终点有关

标量场的梯度有一个重要的性质，即它的旋度恒等于0

$\pmb \nabla\times(\pmb\nabla u) \equiv 0$

也就是说，任何标量场的梯度场一定是无旋场

一个标量场的梯度可以由它的梯度完全确定

对于一个旋度处处为0的矢量场 $\pmb F$ ，总可以把它表示为某一标量场的梯度，即如果 $\pmb\nabla\times\pmb F\equiv0$ ，则存在标量函数 $u$ ，使得

$\pmb F = -\nabla u$

则函数 $u$ 称为无旋场 $\pmb F$ 的标量位函数，简称标量位，负号是为使其电磁场中电场强度 $\pmb E$ 和标量电位 $\varphi$ 的关系一致

设无旋场 $\pmb F$ 的散度为

$\pmb\nabla\cdot\pmb F = g$

其中 $g$ 为已知的标量函数，可得

$\pmb\nabla\cdot(\pmb\nabla u) = -g$

其中 $\pmb\nabla\cdot(\pmb\nabla u)$ 是对标量场 $u$ 的二阶微分运算，称为拉普拉斯运算，记为 $\pmb\nabla\cdot(\pmb\nabla u) = \pmb\nabla^2u$

$\pmb\nabla^2$ 称为拉普拉斯算符，方程

$\pmb\nabla^2u = -g$

称为标量泊松方程，当 $g = 0$ 时称为拉普拉斯方程

无散场的矢量位

如果一个矢量场 $\pmb F$ 的散度处处为0，即

$\pmb\nabla\cdot\pmb F\equiv0$

则称该矢量场为无散场

由散度定理可得，无散场通过任何闭合曲面 $S$ 的通量等于0，即

$\oint_S\pmb F\cdot d\pmb S = \int_v\pmb\nabla\cdot\pmb FdV = 0$

矢量场的散度有一个重要的性质，就是旋度的散度恒等于0，即

$\pmb\nabla\cdot(\pmb\nabla\times\pmb A) = 0$

也就是说，任何矢量场的旋度场一定是无散场

对于一个散度处处为0的矢量场 $\pmb F$ ，总可以表示为某一矢量场的旋度，即如果 $\pmb\nabla\cdot F\equiv0$ ，则存在矢量函数 $\pmb A$ ，使得

$\pmb F = \pmb\nabla\times\pmb A$

函数 $\pmb A$ 称为无散场 $\pmb F$ 的矢量位函数，简称矢量位

定义矢量场的拉普拉斯运算为

$\pmb\nabla^2 A = \pmb\nabla(\pmb\nabla\cdot A) - \pmb\nabla\times(\pmb\nabla\times\pmb A)$

方程

$\pmb\nabla^2A = -\pmb G$

称为矢量泊松方程，在 $\pmb G = 0$ 的区域，则有

$\pmb\nabla^2A = 0$

称为矢量拉普拉斯方程

格林定理

格林第一恒等式定义如下

$\int_V(u\pmb\nabla^2v + \pmb\nabla u\cdot\pmb\nabla v)dV = \oint_S u\pmb\nabla v\cdot\pmb e_ndS$

根据方向导数和梯度的关系，有

$u\pmb\nabla v\cdot\pmb e_n = u\frac{\partial v}{\partial n}$

将格林第一恒等式进行变换，可得

$\int_V(u\pmb\nabla^2v - v\pmb\nabla^2u)dV = \oint_S(u\frac{\partial v}{\partial n} - v\frac{\partial u}{\partial n})dS$

此方程称为格林第二恒等式

亥姆霍兹定理

在有限的区域 $V$ 内，任一矢量场由它的散度，旋度和边界条件（场在空间上的分布）唯一地决定，且可表示为

$\pmb F(\pmb r) = -\pmb\nabla u(\pmb r) + \pmb\nabla\times\pmb A(\pmb r)$

亥姆霍兹定理表明了

矢量场可以由一个标量函数的梯度和一个矢量函数的旋度之和来表示
一个矢量场可以表示为一个无散场和一个无旋场之和
如果区域 $V$ 内矢量场的散度和旋度处处为0，则 $\pmb F$ 由其在边界面 $S$ 上的场分布完全确定
对于无界空间，只要矢量场满足 $|\pmb F|\varpropto 1/{|\pmb r - \pmb r^{'}|}^{1 + \delta}(\delta > 0)$ ，此时矢量场可以由其散度和旋度完全确定

只有在矢量场连续的区域内， $\pmb\nabla\cdot\pmb F$ 和 $\pmb\nabla\times\pmb F$ 才有意义，因为它们都包含对于空间坐标的导数

电磁场的基本规律

电荷守恒定律

基本点电荷的电量为 $e = 1.602\times10^{-9}C$

电荷密度

电荷体密度

单位体积内所含电荷量的大小

电荷面密度

当电荷分布区域的厚度趋于0时，可以将这种电荷分布看作电荷面密度

在电荷体密度有限的表面上，其电荷面密度必然为0

在电荷面密度不为0的表面上，其电荷体密度的值则为无穷大

电荷线密度

当电荷连续分布于横截面积可以忽略的细线上时，电荷体密度和电荷面密度都趋于无穷大，此时需要用电荷线密度进行描述

点电荷

当带电体的尺寸远远小于观察点至带电体的距离时，带电体的形状和其中的电荷分布已经无关紧要了，可以抽象为一个带电荷的点，即点电荷

电流密度

电流密度矢量 $\pmb J(\pmb r,t)$

在垂直于电荷运动的方向上取一个面积元 $\pmb e_n\Delta S$ ， $\pmb e_n$ 为正电荷运动的方向，如果流过面积元的电流为 $\Delta i(\pmb r,t)$ ，则定义电流密度矢量为

$\pmb J(\pmb r,t) = \pmb e_n\lim_{\Delta S\rightarrow0}\frac{\Delta i(\pmb r,t)}{\Delta S} = \pmb e_n\frac{di(\pmb r,t)}{dS}$

面电流密度矢量 $\pmb J_S(\pmb r,t)$

若电荷在一个厚度 $h$ 可以忽略的薄层是运动，所形成的电流称为面分布电流

定义面电流密度矢量为

$\pmb J_S(\pmb r,t) = \pmb e_n\frac{di(\pmb r,t)}{dl}$

线电流

当电荷在一个横截面可以忽略的细线中运动时，可以把电流看作在一根无限细的线上流动，称为线电流

$i = \rho_lv$

其中 $\rho_l$ 为线电流密度， $v$ 是电流速度

电流元

对于线电流 $i$ ，沿电流流动的方向取一个线元矢量 $d\pmb l$ ，将 $id\pmb l$ 称为线电流的电流元

电荷守恒定律和电流连续性方程

电荷守恒定律：在一个与外界没有电荷交换的系统内，正负电荷的代数和在任何物理过程中始终保持不变

电流连续性：单位时间内从闭合面内流出的电荷量等于闭合面所限定的体积内的电荷减少量，即

$\oint_S\pmb J\cdot dS = -\frac{d}{dt}\int_V\rho dV$

此为电流连续性方程的积分形式，经过变换可得

$\pmb\nabla\cdot\pmb J + \frac{\partial\rho}{\partial t} = 0$

此为电流连续性方程的微分形式

对于恒定电流而言，有 $\pmb\nabla\cdot\pmb J = 0$ ，即恒定电流场是一个无散度的场，从任何闭合曲面穿过的恒定电流为0

真空中静电场的基本规则

库仑定律

在电场中放入一个试验电荷 $q_0$ ，设其受到的电场力为 $\pmb F$ ，可定义该点的电场强度矢量 $\pmb E$ 为

$\pmb E = \frac{\pmb F}{q_0}$

库仑定律的方程为

$\pmb F_{12} = \pmb e_{12}\frac{q_1q_2}{4\pi\varepsilon_0R_{12}^2} = \frac{q_1q_2}{4\pi\varepsilon_0R_{12}^3}\pmb R_{12}$

其中 $\pmb e_n$ 是由 $q_1$ 指向 $q_2$ 的单位矢量， $\pmb R_{12} = \pmb r_2 - \pmb r_1$ 是由 $q_1$ 到 $q_2$ 的距离矢量， $\varepsilon_0 = \frac{1}{36\pi}\times 10^{-9}F/m$ ，称为真空的介电常数

静电场的电场力的叠加遵循平行四边形原则

从而可以推导出电场强度表达式为

$\pmb E(\pmb r) = \frac{q}{4\pi\varepsilon_0R^3}\pmb R$

其中 $\pmb R = \pmb r - \pmb r^{'}$ 是源点到场点的距离矢量

静电场的散度和旋度

静电场的高斯定理的微分形式为

$\pmb\nabla\cdot\pmb E = \frac{\rho}{\varepsilon_0}$

积分形式为

$\oint_S\pmb E\cdot dS = \frac{1}{\varepsilon_0}\int_V\rho dV$

静电场的旋度为

$\pmb\nabla\times\pmb E = 0$

所以静电场是无旋场

真空中恒定磁场的基本规律

安培力定律

若一个电量为 $q_0$ 的电荷以速度 $\pmb v$ 在磁场中运动，它所受到的磁场力为

$\pmb F_m = q_0\pmb v\times\pmb B$

因此可得磁感应强度的大小为

B = \lim_{q_0\rightarrow 0}\frac{F_m|_\max}{q_0v}

可得电流元 $Id\pmb l$ 在磁场中受到的磁场力为

$d\pmb F_m = Id\pmb l\times\pmb B$

对于电流元产生的磁场，毕奥-萨伐尔定律为

$\pmb B(\pmb r) = \frac{\mu_0}{4\pi}\oint_C\frac{Id\pmb l'\times\pmb R}{R^3}$

其中 $\pmb R = \pmb r - \pmb r',R = |\pmb r - \pmb r'|$

对于体电流密度为 $\pmb J(\pmb r')$ 的体分布电流，则磁感应强度为

$\pmb B(\pmb r) = \frac{\mu_0}{4\pi}\int_V\frac{\pmb J(\pmb r')\times\pmb R}{R^3}dV'$

同样，对于面电流密度为 $\pmb J_s(\pmb r')$ 的面分布电流，磁感应强度为

$\pmb B(\pmb r) = \frac{\mu_0}{4\pi}\int_S\frac{\pmb J_S(\pmb r')\times\pmb R}{R^3}dS'$

恒定磁场的散度和旋度

恒定磁场的散度为

$\pmb\nabla\cdot\pmb B(\pmb r) = 0$

可得恒定磁场为无散场

恒定磁场的旋度为

$\pmb\nabla\times\pmb B(\pmb r) = \mu_0\pmb J(\pmb r)$

此为安培环路定理的微分形式，其积分形式为

$\oint_C\pmb B(\pmb r)\cdot d\pmb l = \mu_0I$

媒质的电磁特性

电介质的极化特性

空间的电场强度 $\pmb E$ 是自由电荷产生的电场强度 $\pmb E_0$ 与极化电荷产生的电场强度 $\pmb E_p$ 的叠加，即

$\pmb E = \pmb E_0 + \pmb E_p$

极化强度矢量 $\pmb P$ 定义如下

$\pmb P = \lim_{\Delta V\rightarrow 0}\frac{\sum_i\pmb p_i}{\Delta V}$

其中 $\pmb p_i = q_i\pmb l_i$ 表示体积 $\Delta V$ 中第 $i$ 个分子的电偶极矩，极化强度矢量的单位是 $C/m^2$

若电介质内各点的 $\pmb P$ 相同，则称为均匀极化，否则为非均匀极化

无论是均匀极化还是非均匀极化，电介质的表面都会出现面分布的极化电荷

但是对于均匀极化，电介质内部不会出现体分布的极化电荷，而非均匀极化会出现体分布的极化电荷

电介质表面上的极化电荷面密度为

$\rho_{SP} = \pmb P\cdot\pmb e_n$

我们定义电位移矢量为

$\pmb D = \varepsilon_0\pmb E + \pmb P$

其单位为 $C/m^2$

电介质中高斯定理的积分形式为

$\oint_S \pmb D\cdot d\pmb S = q$

它表明电位移矢量穿过任一闭合面的通量等于该闭合面内总的自由电荷，而与极化电荷无关

电介质中高斯定理的微分形式为

$\pmb\nabla\cdot\pmb D = \rho$

它表明电介质内任一点的电位移矢量的散度等于该点的自由电荷体密度，电位移矢量线从正的自由电荷出发，终于负的自由电荷

虽然电位移矢量的通量和散度都只与自由电荷有关，但不能认为电位移矢量只由自由电荷产生而与极化电荷无关

实际上电位移矢量是由自由电荷和极化电荷共同产生的电场强度矢量以及极化强度矢量所决定的

因此，电介质中静电场的基本方程的积分形式为

$\begin{cases}\oint_S\pmb D\cdot d\pmb S = q\\\\\oint_C\pmb E\cdot d\pmb l = 0\end{cases}$

对于相同的电场强度 $\pmb E$ ，不同电介质的极化情况是不相同的

大多数常见的电介质在电场的作用下发生极化时，其极化强度矢量与电场强度矢量成正比，表示为

$\pmb P = \varepsilon_0\chi_e\pmb E$

其中 $\chi_e$ 称为电介质的电极化率，是一个正实数

这类电介质的极化强度矢量 $\pmb P$ 与电场强度矢量 $\pmb E$ 的方向相同，电极化率和电场强度的方向无关，称为各向同性电介质

电极化率和电场强度大小无关的电介质称为线性介质，电极化率的值随电场强度的大小的不同而变化的电介质称为非线性介质

在电场强度不是很强的情况下，多数介质都是线性的，但是在强电场的作用下就可能呈现出非线性特性

对于各向同性介质，有

$\begin{aligned} \pmb D &=\varepsilon_0\pmb E + \chi_e\varepsilon_0\pmb E \\ &=\varepsilon\pmb E \end{aligned}$

其中 $\varepsilon = \varepsilon_0\varepsilon_r$ 称为电介质的介电常数， $\varepsilon_r = 1 + \chi_e$ 为电介质的相对介电常数

上述公式表示了各向同性电介质的本构关系，此关系表明在各向同性电介质中，电位移矢量 $\pmb D$ 和电场强度 $\pmb E$ 的方向相同

若电介质是线性的，则介电常数·与电场强度的大小无关，电位移矢量与电场强度的大小成正比

若电介质是均匀的，则介电常数处处相等，若是非均匀的，则介电常数是空间坐标的函数

对于各向异性电介质，电位移矢量和电场强度的方向通常是不相同的

磁介质的磁化特性

电子在自己的轨道上以恒定速度绕原子核运动，形成一个环形电流，它相当于一个磁偶极子，将其磁矩称为自旋磁矩

通常可以忽略原子的自旋，将磁介质的每个分子（或原子）等效于一个环形电流，称为分子电流/束缚电流，分子电流的磁矩称为分子磁矩，用 $\pmb p_m$ 表示，定义为

$\pmb p_m = i\pmb\Delta S$

其中 $i$ 为分子电流， $\pmb\Delta S = \pmb e_n\Delta S$ 为分子电流所围的面积元矢量，其方向 $\pmb e_n$ 与 $i$ 流动的方向成右手螺旋关系

不同磁介质的分子磁矩不同，可能为0，可能不为0

磁介质可以分为顺磁体（分子磁矩不为0），抗磁体（分子磁矩为0）和铁磁体（磁畴）三种

描述磁介质磁化程度的物理量称为磁化强度矢量，用 $\pmb M$ 表示，定义为单位体积内分子磁矩的矢量和

$\pmb M = \lim_{\Delta V\rightarrow0}\frac{\sum_i\pmb p_{mi}}{\Delta V}$

其中 $\pmb p_{mi}$ 表示体积 $\Delta v$ 内第 $i$ 个分子的磁矩， $\pmb M$ 是一个矢量函数，单位是 $A/m$ ，若磁介质当中各点 $\pmb M$ 相同，称之为均匀磁化，否则称为非均匀磁化

磁介质被磁化后，其内部和表面可能出现宏观电流分布，称为磁化电流，可以表示为磁化电流密度的积分，即

$I_M = \int_S\pmb J_M\cdot d\pmb S$

$\pmb J_M = \pmb\nabla\times\pmb M$

磁化面电流密度矢量为

$\pmb J_{SM} = \pmb M\times\pmb e_n$

其中 $\pmb e_n$ 为磁介质表面的法向单位矢量

磁介质被磁化后，磁感应强度等于传导电流 $I$ 在真空中产生的磁感应强度和磁化电流在真空中产生的磁感应强度的叠加，即

$\pmb B = \pmb B_0 + \pmb B_M$

安培环路定理的积分形式为

$\oint_C\pmb H\cdot d\pmb l = I$

它表明磁场强度沿任意闭合路径的环量等于与该闭合路径交链的传导电流

其中 $\pmb H$ 为磁场强度，如下所示

$\pmb H = \frac{1}{\mu_0}\pmb B - \pmb M$

由斯托克斯定理可得安培环路定理的微分形式

$\pmb\nabla\times\pmb H = \pmb J$

由此可见，在磁介质中任一点的磁场强度等于该点的传导电流密度

磁化强度矢量 $\pmb M$ 与磁场强度矢量 $\pmb H$ 和磁介质的物理特性有关

实验表明，对于线性和各向同性磁介质，磁化强度和磁场强度成正比，表示为

$\pmb M = \chi_m\pmb H$

其中 $\chi_m$ 称为磁介质的磁化率，不同的磁介质有不同的磁化率

由上式可得

$\pmb B = (1 + \chi_m)\mu_0\pmb H = \mu_r\mu_0\pmb H = \mu H$

此式称为各向同性磁介质的本构关系，其中 $\mu = \mu_r\mu_0$ 称为磁介质的磁导率， $\mu_r$ 称为磁介质的相对磁导率

真空中 $\chi_m = 0,\mu_r = 1$ 无磁化效应， $\pmb M = 0,\pmb B = \mu_0\pmb H$

$\mu_r > 1,\chi_m > 0$ 的磁介质是顺磁体， $\mu_r < 1,\chi_m < 0$ 的磁介质是抗磁体

顺磁体和抗磁体的磁化效应都很弱，对于铁磁体， $B$ 和 $H$ 的关系是非线性的， $\mu_r$ 值可以很大

导电媒质的传导特性

导电媒质内部有许多能自由移动的带电粒子，它们在外电场的作用下可以定向移动形成电流

在线性和各向同性的导电媒质内，任意一点的电流密度矢量 $\pmb J$ 与该点的电场强度 $\pmb E$ 成正比，表示为

$\pmb J = \sigma\pmb E$

其中 $\sigma$ 称为媒质的电导率，上式是线性各向同性导电媒质的本构关系，也是欧姆定律的微分形式

电导率的值和媒质有关，且随温度变化

焦耳定律的微分形式为

$p_L = \frac{dP_L}{dV} = \pmb J\cdot\pmb E$

其中 $p_L$ 为单位体积的损耗功率， $\pmb J = \rho\pmb v$ ，其中 $\rho$ 为电荷体密度， $\pmb v$ 为电荷的平均速度

焦耳定律的积分形式为

$P_L = \int_Vp_LdV = \int_V\pmb J\cdot\pmb E dV$

对于线性和各向同性的导体，焦耳定理的微分和积分形式可分别表示为

$p_L = \sigma\pmb E\cdot\pmb E = \sigma E^2$

$P_L = \int_V\sigma E^2dV$

电磁感应定律和位移电流

法拉第电磁感应定律

实验表明，感应电动势与穿过回路所围面积的磁通量的时间变化率成正比，即

$\mathcal E_{in} = -\frac{d\Phi}{dt} = -\frac{d}{dt}\int_S\pmb B\cdot d\pmb S$

感应电流产生的磁通总是对原磁通的变化起阻碍作用

在空间中的总电场由感应电场和库伦电场的叠加

$\pmb E = \pmb E_{in} + \pmb E_C$

由于有 $\oint_C\pmb E\cdot d\pmb l = 0$ ，则有

$\oint_C\pmb E\cdot d\pmb l = -\frac{d}{dt}\int_S\pmb B\cdot d\pmb S$

这就是推广之后的法拉第电磁感应定律的积分形式

如果回路是静止的，则穿过回路的磁场会随时间变化，此时有

$\oint_C\pmb E\cdot d\pmb l = -\int_S\frac{\partial \pmb B}{\partial t}\cdot d\pmb S$

这就是静止回路位于时变磁场当中的法拉第电磁感应定律的积分形式

而可由斯托克斯定理推导出其微分形式

$\pmb\nabla\times\pmb E = -\frac{\partial\pmb B}{\partial t}$

法拉第电磁感应定律积分形式的一般形式为

$\oint_C\pmb E\cdot d\pmb l = -\int_S\frac{\partial\pmb B}{\partial t}\cdot d\pmb S + \oint_C(\pmb v\times\pmb B)\cdot d\pmb l$

其微分形式为

$\nabla\times\pmb E = -\frac{\partial B}{\partial t} + \pmb\nabla\times(\pmb v\times\pmb B)$

位移电流

之前的 $\pmb\nabla\times\pmb H = \pmb J$ 不适用于时变电磁场，需要进行修正

时变条件下的电流连续性方程为

$\pmb J_d = \frac{\partial\pmb D}{\partial t}$

其中 $\pmb J_d$ 称为位移电流密度

修正后的公式如下

$\pmb\nabla\times\pmb H = \pmb J + \frac{\partial\pmb D}{\partial t}$

时变电磁场当中安培环路定理的积分形式如下

$\oint_C\pmb H\cdot d\pmb l = \int_S\left(\pmb J + \frac{\partial\pmb D}{\partial t}\right)\cdot d\pmb S$

需要说明的是位移电流没有通常电流的概念，由 $\pmb D = \varepsilon_0\pmb E + \pmb P$ 可知

$\frac{\partial\pmb D}{\partial t} = \varepsilon_0\frac{\partial\pmb E}{\partial t} + \frac{\partial\pmb P}{\partial t}$

其中， $\frac{\partial\pmb P}{\partial t}$ 是由于介质分子的极化电荷随时间变化而引起的，称为极化电流，而 $\varepsilon_0\frac{\partial\pmb E}{\partial t}$ 则仅表示电场随时间的变化，并不对应任何电荷的运动

麦克斯韦方程组

麦克斯韦方程组的积分和微分形式

麦克斯韦方程组的积分形式为

$\oint_C\pmb H\cdot d\pmb l = \int_S\pmb J\cdot d\pmb S + \int_S\frac{\partial\pmb D}{\partial t}\cdot d\pmb S\tag{1}$

$\oint_C\pmb E\cdot d\pmb l = -\int_S\frac{\partial\pmb B}{\partial t}\cdot d\pmb S \tag{2}$

$\oint_S\pmb B\cdot d\pmb S = 0\tag{3}$

$\oint_S\pmb D\cdot d\pmb S = \int_V\rho dV\tag{4}$

式(1)的含义是磁场强度沿任意闭合曲线的环量等于穿过以该闭合曲线为周界的任意曲面的传导电流和位移电流之和

式(2)的含义是电场强度沿任意闭合曲线的环量等于穿过以该闭合曲线为周界的任一曲面的磁通量变化率的负值

式(3)的含义是穿过任意闭合曲面的磁感应强度的通量恒等于0

式(4)的含义是穿过任意闭合曲面的电位移的通量等于该闭合面所包围的自由电荷的代数和

麦克斯韦方程组的微分形式为

$\pmb\nabla\times\pmb H = \pmb J + \frac{\partial\pmb D}{\partial t}\tag{5}$

$\pmb\nabla\times\pmb E = -\frac{\partial\pmb B}{\partial t}\tag{6}$

$\pmb\nabla\cdot\pmb B = 0\tag{7}$

$\pmb\nabla\cdot\pmb D = \rho\tag{8}$

式(5)表明传导电流和时变电场要产生磁场，都是磁场的涡旋源

式(6)表明时变磁场要产生电场，是电场的涡旋源

式(7)表明磁场是无散场，磁感应线是闭合曲线

式(8)表明电荷要产生电场，是电场的散度源

由麦克斯韦方程组可以推导出恒定磁场方程和静电场方程如下

$\pmb\nabla\times\pmb H = \pmb J$

$\pmb\nabla\cdot\pmb B = 0$

$\pmb\nabla\times\pmb E = 0$

$\pmb\nabla\cdot\pmb D = \rho$

媒质的本构关系

媒质的本构关系也称为电磁场的辅助方程，在线性各向同性的导电媒质当中，本构关系为

$\pmb D = \varepsilon\pmb E$

$\pmb B = \mu\pmb H$

$\pmb J = \sigma\pmb E$

其中 $\pmb J$ 表示在电场作用下在导电媒质中形成的传导电流密度

若媒质是均匀的且参数不随时间变化，则可以得到以下用 $\pmb E,\pmb H$ 表示的麦克斯韦方程组

$\pmb\nabla\times\pmb H = \pmb J_e + \sigma\pmb E + \varepsilon\frac{\partial\pmb E}{\partial t}$

$\pmb\nabla\times\pmb E = -\mu\frac{\partial\pmb H}{\partial t}$

$\pmb\nabla\cdot\pmb H = 0$

$\pmb\nabla\cdot\pmb E = \frac{\rho}{\varepsilon}$

其中 $\pmb J_e$ 为外加的电流密度

准静态电磁场

在时变的情况下，如果电磁场随时间变化非常缓慢时，若可以忽略 $\frac{\partial\pmb B}{\partial t}$ 或 $\frac{\partial\pmb D}{\partial t}$ 时，则这种电磁场称为准静态电磁场

它们的特点是电场和磁场都随时间变化，但是却具有一些静态场的性质

根据忽略的 $\frac{\partial\pmb B}{\partial t}$ 或 $\frac{\partial\pmb D}{\partial t}$ 的不同，可以分为电准静态电磁场和磁准静态电磁场

电准静态电磁场

此时麦克斯韦方程组可以近似为

$\pmb\nabla\times\pmb H = \pmb J + \frac{\partial\pmb D}{\partial t}$

$\pmb\nabla\times\pmb E \approx 0$

$\pmb\nabla\cdot\pmb B = 0$

$\pmb\nabla\cdot\pmb D = \rho$

可以利用静电场的公式去求解 $\pmb E$ 和 $\pmb D$

磁准静态电磁场

此时麦克斯韦方程组可以近似为

$\pmb\nabla\times\pmb H \approx \pmb J$

$\pmb\nabla\times\pmb E = -\frac{\partial\pmb B}{\partial t}$

$\pmb\nabla\cdot\pmb B = 0$

$\pmb\nabla\cdot\pmb D = \rho$

可以利用恒定磁场的公式去求解 $\pmb B$ 和 $\pmb H$

电磁场的边界条件

边界条件的一般形式

设两种媒质的分界面为光滑曲面，分界面上任一点 $P$ 处的法向量 $\pmb e_n$ 由媒质2指向媒质1

一般表达式为

$\pmb e_n\times(\pmb H_1 - \pmb H_2) = \pmb J_S$

$\pmb e_n\times(\pmb E_1 - \pmb E_2) = 0$

$\pmb e_n\cdot(\pmb B_1 - \pmb B_2) = 0$

$\pmb e_n\cdot(\pmb D_1 - \pmb D_2) = \rho_S$

其中 $\pmb J_S$ 为分界面上的传导面电流密度， $\rho_S$ 为分界面上的自由电荷面密度

若两种媒介的电导率均为有限值，则 $\pmb J_S = \lim_{\Delta h\rightarrow0}J\Delta h = 0$ ，即分界面上不存在面电流分布，可得

$\pmb e_n\times(\pmb H_1 - \pmb H_2) = 0$

当分界面上没有自由电荷面密度时，有

$\pmb e_n\cdot(\pmb D_1 - \pmb D_2) = 0$

理想导体表面上的边界条件

设媒质2为理想导体，则在时变情况下， $\pmb E_2,\pmb D_2,\pmb B_2,\pmb H_2$ 均为0，则有

$\pmb e_n\times\pmb H_1 = \pmb J_S$

$\pmb e_n\times\pmb E_1 = 0$

$\pmb e_n\cdot\pmb B_1 = 0$

$\pmb e_n\cdot\pmb D_1 = \rho_S$

理想介质分界面上的边界条件

设媒质1和媒质2为两种不同的理想介质，由于理想介质当中不存在自由电子，则有

$\pmb e_n\times(\pmb H_1 - \pmb H_2) = 0$

$\pmb e_n\times(\pmb E_1 - \pmb E_2) = 0$

$\pmb e_n\cdot(\pmb B_1 - \pmb B_2) = 0$

$\pmb e_n\cdot(\pmb D_1 - \pmb D_2) = 0$

静态电磁场及其边值问题的解

静电场分析

静电场的基本方程和边界条件

静电场的基本方程的积分形式为

$\begin{cases}\oint_S\pmb D\cdot d\pmb S = \int_V\rho dV\\\\\oint_C\pmb E\cdot d\pmb l = 0\end{cases}$

微分形式为

$\begin{cases}\pmb\nabla\cdot\pmb D = \rho\\\\\pmb\nabla\times\pmb E = 0\end{cases}$

在线性，各向同性的电介质中，本构关系为

$\pmb D = \varepsilon\pmb E$

静电场的边界条件的一般形式为

$\pmb e_n\times(\pmb E_1 - \pmb E_2) = 0 \quad或\quad E_{1t} = E_{2t}$

$\pmb e_n\cdot(\pmb D_1 - \pmb D_2) = \rho_S \quad或\quad D_{1n} - D_{2n} = \rho_S$

电位函数

电位和电位差

电场强度矢量 $\pmb E$ 可以表示为标量函数 $\varphi$ 的梯度，即

$\pmb E(\pmb r) = -\pmb\nabla\varphi(\pmb r)$

其中的 $\varphi(\pmb r)$ 称为静电场的电位函数，简称为电位

电位函数不是唯一的，可以任意加上一个常数，电场强度 $\pmb E$ 保持不变

可以得到电位的计算公式：在线性，各向同性的无界均匀媒质中，点电荷 $q$ 的产生的电场的电位函数为

$\varphi(\pmb r) = \frac{q}{4\pi\varepsilon R} + c$

其中 $c$ 为任意常数

点 $P,Q$ 之间的电位差的物理意义是：把一个单位正电荷从点 $P$ 沿任意路径移动到点 $Q$ 的过程中，电场力所做的功

若选定 $Q$ 点为电位参考点，则 $P$ 点的电位为

$\varphi(P) = \int^Q_P\pmb E\cdot d\pmb l$

若场源电荷分布在有限区域，通常选定无限远处为电位参考点，即

$\varphi(P) = \int^\infty_P\pmb E\cdot d\pmb l$

静电位的微分方程和边界条件

静电位满足标量泊松方程

$\pmb\nabla^2\varphi(\pmb r) = -\frac{\rho(\pmb r)}{\varepsilon}$

在无自由电荷分布的区域中，即 $\rho = 0$ ，则电位函数满足拉普拉斯方程

$\pmb\nabla^2\varphi(\pmb r) = 0$

在静电场当中，由于导体的内部的电场为0，所以导体为等位体，导体表面为等位面

因此，在导体表面上的电位边界条件为

$\begin{cases}\varphi = 常数\\\\\varepsilon\frac{\partial\varphi}{\partial n} = -\rho_S\end{cases}$

导体系统的电容

电容器的电容定义为电荷量和电压之比

$C = \frac{q}{U}$

单位为法拉（F）

一个孤立导体可以看作是与无穷远处的另一个导体构成的电容器，其电容大小和电荷量以及电位有关，为

$C = \frac{q}{\varphi}$

在计算电容器的电容时，常常采用以下的计算步骤

假定两导体上分别带电荷 $+q$ 和 $-q$
根据假定的电荷求出电场强度 $\pmb E$
由 $\int^2_1\pmb E\cdot d\pmb l$ 求电位差 $U$
求出比值 $C = \frac q U$

设空间中存在 $N+1$ 个导体，各导体所带的电荷量分别为 $q_0,q_1,q_2,\cdots,q_N$ 且所有导体的电荷量之和为0

则称该多导体为静电独立系统

若空间中的介质是线性的，则各导体的电位与各导体上的电荷之间也是线性关系

如果把电荷量为 $q_0$ 的导体作为电位参考点，则其余 $N$ 个导体的电位 $\varphi_1,\varphi_2,\cdots,\varphi_N$ 可表示为

$\begin{cases}\varphi_1 = \alpha_{11}q_1 + \alpha_{12}q_2 + \cdots+\alpha_{1N}q_N\\\\\varphi_2 = \alpha_{21}q_1 + \alpha_{22}q_2 + \cdots+\alpha_{2N}q_N\\\\\cdots\\\\\varphi_N = \alpha_{N1}q_1 + \alpha_{N2}q_2 + \cdots+\alpha_{NN}q_N\end{cases}$

其中 $\alpha_{ij}$ 称为电位系数， $\alpha_{ii}$ 为自电位系数， $\alpha_{ij}$ 为互电位系数

在计算 $\alpha_{ij}$ 的时候，可以令 $q_j\neq0$ ，而其余导体的电荷都为0，即

$\alpha_{ij} = \frac{\varphi_i}{q_j}(q_1 = \cdots = q_N = 0)$

所有的电位系数都具有对称性，即 $\alpha_{ij} = \alpha_{ji}$

电容系数和部分电容暂且不写

静电场的能量

电场能量的公式为

$W_e = \frac{1}{2}CU^2 = \frac{1}{2}qU$

对于线性和各向同性介质，有 $\pmb D = \varepsilon\pmb E$ ，则有

$W_e = \frac{1}{2}\int_V\varepsilon E^2dV$

静电力

$F_i = -\frac{\partial W_e}{\partial g_i}(q为常数，dg_i为虚位移)$

导电媒质中的恒定电场分析

恒定电场的基本方程和边界条件

恒定电场的基本方程

由麦克斯韦方程组可以得出恒定电场满足的方程为

$\pmb\nabla\cdot\pmb D = \rho$

$\pmb\nabla\times\pmb E = 0$

电场强度沿任一闭合路径的线积分恒为0，即

$\oint_C \pmb E\cdot d\pmb l = 0$

由于恒定电场不随时间变化，所以电荷的分布也不随时间变化，即 $\frac{\partial\rho}{\partial t} = 0$

根据电流连续性方程可得

$\oint_S\pmb J\cdot d\pmb S = 0$

相应的微分形式为

$\pmb\nabla\cdot\pmb J = 0$

在线性，各向同性的导电媒质当中，本构关系为

$\pmb D = \varepsilon\pmb E$

$\pmb J = \sigma\pmb E$

恒定电场也可以用电位梯度来表示

$\pmb E = -\pmb\nabla\varphi$

在均匀导电媒质当中（ $\sigma = 常数$ ）当中，电位函数满足拉普拉斯方程，即

$\pmb\nabla^2\varphi = 0$

导电媒质当中的电荷体密度为

$\rho = \pmb J\cdot\pmb\nabla\left(\frac{\varepsilon}{\sigma}\right)$

由此可见，在恒定电场当中，只有非均匀的导电媒质内部才可能存在电荷分布，而均匀导电媒质内的电荷密度处处为0，电荷只能分布在媒质的分界面上

恒定电场的边界条件

恒定电场的电位函数的边界条件是

$\varphi_1 = \varphi_2$

$\sigma_1\frac{\partial\varphi_1}{\partial n} = \sigma_2\frac{\partial\varphi_2}{\partial n}$

恒定磁场分析

恒定磁场的基本方程和边界条件

由麦克斯韦方程组可以得出恒定磁场的基本方程的积分形式为

$\begin{cases}\oint_C\pmb H\cdot d\pmb l = \int_S\pmb J\cdot d\pmb S\\\\\oint_S\pmb B\cdot d\pmb S = 0\end{cases}$

微分形式为

$\begin{cases}\pmb\nabla\times\pmb H = \pmb J\\\\\pmb\nabla\cdot\pmb B = 0\end{cases}$

这表明恒定磁场是无源有旋场，恒定电流是产生恒定磁场的涡旋源，磁力线是与源电流相交链的闭合曲线

线性，各向同性的磁介质的本构关系为

$\pmb B = \mu\pmb H$

在分界面上的 $\pmb B$ 是连续的

矢量磁位

电磁场的位函数是根据电磁场性质引入的辅助函数，其数学定义与电磁场性质相关

$\pmb B = \pmb\nabla\times\pmb A(\pmb r)$

恒定磁场中采用的规范条件为库伦规范

$\pmb\nabla\cdot\pmb A(\pmb r) = 0$

规范条件是人为引入的限定条件

矢量位的泊松方程为

$\pmb\nabla^2\pmb A = -\mu_0\pmb J$

在无源区， $\pmb J = 0$ ，则有矢量位的拉普拉斯方程

$\pmb\nabla^2\pmb A = 0$

矢量磁位可以通过矢量分解来求解

$A_x = \frac{\mu_0}{4\pi}\int_V\frac{J_xdV}{R}$

$A_y = \frac{\mu_0}{4\pi}\int_V\frac{J_ydV}{R}$

$A_z = \frac{\mu_0}{4\pi}\int_V\frac{J_zdV}{R}$

电感

磁通的为通过面积 $S$ 的磁感应强度 $B$

$\Phi = \int_S\pmb B\cdot d\pmb S = \oint_C\pmb A\cdot d\pmb l$

磁链是指与所有电流回路铰链的总磁通

单匝细线圈的磁链 $\Psi = \Phi$

多匝细线圈密绕的磁链 $\Psi = n\Phi$

粗导线回路的磁链 $\Psi = \Psi_o + \Psi_i$

其中 $\Psi_o$ 为外磁链， $\Psi_i$ 为内磁链

电流回路的电感是穿过某电流回路的磁链与回路中电流强度之比

$L = \frac\Phi I$

若某回路 $C$ 载流为 $I$ ，其产生的磁场穿过回路自身 $C$ 所形成的自感磁链为，则定义回路 $C$ 的自感系数为

$L = \frac\Psi I\quad(单位为H)$

自感磁链是回路载流I在回路内自已产生的

回路自感仅与回路自身的几何形状、尺寸和媒质磁导率

有关，与回路中载流无关

若回路为N匝线圈密绕，则L = N^2L_0\quad\text{L_0为单匝线圈电感}

若回路导线直径较粗，则回路自感为内自感和外自感之和

$L = L_o + L_i$

其中 $L_o$ 为回路外自感， $L_i$ 为回路内自感

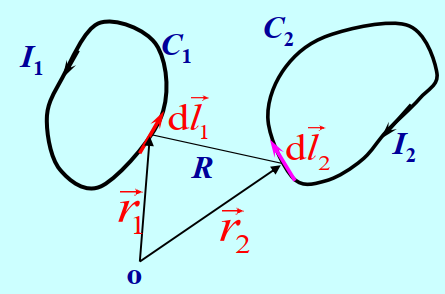
回路 $C_1$ 与回路 $C_2$ 交链的磁通量为 $\Psi_{21}$ ，则回路 $C_1$ 对 $C_2$ 的互感系数为

$M_{21} = \frac{\Psi_{21}}{I_1}$

同理，回路 $C_2$ 对 $C_1$ 的互感系数为

$M_{12} = \frac{\Psi_{12}}{I_2}$

$M_{12} = \frac{\Psi_{12}}{I_2} = \frac{\mu}{4\pi}\oint_{C_1}\oint_{C_2}\frac{d\pmb l_2\cdot d\pmb l_1}{R_{21}}$

互感的大小只与回路几何性质、相对位置和周围介质有关

$M_{21} = M_{12} = M$

恒定磁场的能量

若电流为体电流分布，则其在空间中产生的磁能为

$W_m = \frac 12\int_V\pmb J\cdot\pmb AdV$

其中 $\pmb A$ 为体电流 $\pmb J$ 在 $dV$ 处产生的磁位

$V$ 为整个空间

上式只适用于恒定磁场

被积函数 $\displaystyle\frac 12\pmb J\cdot\pmb A$ 不代表能量密度

对于 $N$ 个回路系统， $i$ 回路自感为 $L_{ii}$ ， $i$ 回路与 $j$ 回路间互感为 $L_{ij}$ ， $i$ 回路电流为 $I_i$ ，则磁回路系统的磁场能量为

$W_m = \frac 12\sum^N_{i = 1}\sum^N_{j = 1}L_{ij}I_iI_j$

磁场的能量密度为

$w_m = \frac 12\pmb B\cdot\pmb H$

对应的磁场能量为

$W_m = \frac 12\int_V\pmb B\cdot\pmb HdV$

积分区域为电场所在的整个空间

时变电磁场

波动方程

电场强度矢量和磁场强度矢量满足的波动方程为

$\pmb\nabla^2\pmb E - \mu\varepsilon\frac{\partial^2\pmb E}{\partial t^2} = \mu\frac{\partial\pmb J}{\partial t} + \frac{1}{\varepsilon}\pmb\nabla\pmb\rho$

$\pmb\nabla^2\pmb H - \mu\varepsilon\frac{\partial^2\pmb H}{\partial t^2} = -\pmb\nabla\times\pmb J$

在无源区， $\rho = 0,\pmb J = 0$ ，则波动方程为

$\pmb\nabla^2\pmb E - \mu\varepsilon\frac{\partial^2\pmb E}{\partial t^2} = 0$

$\pmb\nabla^2\pmb H - \mu\varepsilon\frac{\partial^2\pmb H}{\partial t^2} = 0$

电磁场的位函数

矢量位和标量位

因为

$\pmb\nabla\cdot\pmb B = 0$

则可以将磁场 $\pmb B$ 表示为一个矢量函数 $\pmb A$ 的旋度，即

$\pmb B = \pmb\nabla\times\pmb A$

其中的 $\pmb A$ 则称为电磁场的矢量位

同样的，可以用一个标量函数 $\varphi$ 的梯度来表示电场强度矢量 $\pmb E$

通常规定矢量位 $\pmb A$ 的散度为

$\pmb\nabla\cdot\pmb A = -\mu\varepsilon\frac{\partial\varphi}{\partial t}$

此式称为洛伦兹条件

达朗贝尔方程

在洛伦兹条件下，矢量位和标量位满足的微分方程称为达朗贝尔方程

$\pmb\nabla^2\pmb A - \mu\varepsilon\frac{\partial^2\pmb A}{\partial t^2} = -\mu\pmb J$

$\pmb\nabla^2\varphi - \mu\varepsilon\frac{\partial^2\varphi}{\partial t^2} = -\frac{1}{\varepsilon}\rho$

电磁能量守恒定律

电磁能量密度：单位体积中电磁场的能量，为电场能量和磁场能量之和

$w = w_e + w_m = \frac{1}{2}\left(\varepsilon E^2 + \mu H^2\right)$

体积 $V$ 内总能量为

$W = \int_V\left(\frac 12\pmb E\cdot\pmb D + \frac 12\pmb H\cdot\pmb B\right)dV$

坡印廷定理物理意义：单位时间内流入体积 $V$ 内的电磁能量等于体积 $V$ 内增加的电磁能量与体积 $V$ 内损耗的电磁能量之和

坡印廷定理微分形式：

$-\pmb\nabla\cdot(\pmb E\times\pmb H) = \pmb E\cdot\pmb J + \frac{\partial}{\partial t}\left(\frac 12\pmb E\cdot\pmb D + \frac 12\pmb H\cdot\pmb B\right)$

积分形式：

$-\oint_S(\pmb E\times\pmb H)\cdot d\pmb S(流入体积V的电磁功率 ) = \frac{d}{dt}\int_V\left(\frac 12\pmb E\cdot\pmb D + \frac 12\pmb H\cdot\pmb B\right)dV(体积V内增加的电磁功率 ) + \int_V\pmb E\cdot\pmb JdV(体积V内损耗的电磁功率 )$

坡印廷矢量(电磁能流密度矢量)

坡印廷矢量的物理含义：通过垂直于能量传输方向单位面积的电磁功率（功率流密度）

$\pmb S(t) = \pmb E(t)\times\pmb H(t)$

上式与时间有关，故也称瞬时坡印廷矢量

平均坡印廷矢量：将瞬时形式坡印廷矢量在一个周期内取平均

$\pmb S_{av} = \frac 1T\int^T_0\pmb S(t)dt = \frac 1T\int^T_0\pmb E(t)\times\pmb H(t)dt$

瞬时坡印廷矢量反映某时刻的电磁能量流动情况

平均坡印廷矢量反映一个时间周期内的电磁能量传递情况

平均坡印廷矢量与时间无关

时谐电磁场

时谐电磁场是场量按正弦规律变化的电磁场，也叫正弦电磁场，表达式为

$\pmb E(\pmb r,t) = \pmb E_0\cos[\omega t + \phi(\pmb r)]$

$\pmb H(\pmb r,t) = \pmb H_0\cos[\omega t + \phi(\pmb r)]$

时谐电磁场可以通过复数形式来分离电磁场的空间变化和时间变化

$A(\pmb r,t) = A_0(\pmb r)\cos[\omega t + \phi(\pmb r)] =Re\{A_0(\pmb r)e^{j\phi(\pmb r)}e^{j\omega t}\} = Re[A(\pmb r)e^{j\omega t}]$

场量的复数形式转换为实数形式的方法

$\pmb E = \pmb E_0e^{j\varphi}\stackrel{\times e^{j\omega t}}{\longrightarrow}\pmb E_0e^{j(\omega t + \varphi)}\stackrel{取实部}{\longrightarrow}\pmb E_0\cos(\omega t + \varphi)$

在时谐电磁场当中，对于时间的求导运算为

$\frac{\partial}{\partial t}\longleftrightarrow j\omega$

$\frac{\partial^2}{\partial t^2}\longleftrightarrow -\omega^2$

可得麦克斯韦方程组的复数形式

$\begin{cases}\pmb\nabla\times\pmb H(\pmb r) = \pmb J(\pmb r) + j\omega\pmb D(\pmb r)\\\\\pmb\nabla\times\pmb E(\pmb r) = -j\omega\pmb B(\pmb r)\\\\\pmb\nabla\cdot\pmb D(\pmb r) = \pmb\rho(\pmb r)\\\\\pmb\nabla\cdot\pmb B(\pmb r) = 0\end{cases}$

补充：

$\pmb\nabla\cdot\pmb J(\pmb r) = -j\omega\rho(\pmb r)$

亥姆霍兹方程

在无源区，有

$\begin{cases}\pmb\nabla^2\pmb E + k^2\pmb E = 0\\\\\pmb\nabla^2\pmb H + k^2\pmb H = 0\end{cases}$

其中 $k = \omega\sqrt{\mu\varepsilon}$

时谐电磁场的能量和坡印廷矢量

在复数形势下，瞬时坡印廷矢量的表达式为

$\pmb S(\pmb r,t) = \pmb E(\pmb r,t)\times\pmb H(\pmb r,t) = Re[\pmb E(\pmb r)e^{j\omega t}]\times Re[\pmb H(\pmb r)e^{j\omega t}]$

平均坡印廷矢量的表达式为

$\pmb S_{av}(\pmb r) = \frac 12 Re[\pmb E(\pmb r)\times\pmb H^\ast(\pmb r)]$

均匀平面波在无界媒质中的传播

理想介质中的均匀平面波

电磁波场量的求解

通过波动方程求解会过于复杂，我们通常会采用适当建系的方法来简化运算

平面波的等相位面为x-y平面
平面波的传播方向为z轴方向
电场矢量方向沿坐标轴方向，如x向

这样就可以让 $\pmb E$ 只随着 $z$ 坐标变化而变化

方程

$\pmb\nabla^2\pmb E + k^2\pmb E = 0$

的通解为

$E = E^+_m\cos(\omega t - kz) + E^-_m\cos(\omega t + kz)$

对于

$\pmb E = \pmb e_x\pmb E^-_me^{jkz}$

其相伴的磁场为

$\pmb H = \frac{1}{\eta}(-\pmb e_z)\times\pmb E$

其中

$\eta = \sqrt{\frac{\mu}{\varepsilon}}$

理想介质中均匀平面波的电场与磁场相互正交，且相位相同

对于 $z$ 向波的平面波函数，有以下结论

$e^{-jkz}$ 表示从 $+z$ 方向传播的均匀平面波函数

$e^{jkz}$ 表示从 $-z$ 方向传播的均匀平面波函数

无界理想媒质中均匀平面波的传播特性

波长是空间相位差为 $2\pi$ 的两个波阵面的间距，即

$k\lambda = 2\pi\longrightarrow\lambda = \frac{2\pi}{k} = \frac{1}{f\sqrt{\mu\varepsilon}}$

相位常数：表示波传播单位距离的相位变化

$k = \frac{2\pi}{\lambda}$

$k$ 的大小等于空间距离 $2\pi$ 内所包含的波长数目，因此也称为波数

波矢量 $\pmb k$ ：大小等于相位常数，方向为电磁波传播方向

相速：电磁波的等相位面在空间中的移动速度

$v_p = \frac{dz}{dt} = \frac{\omega}{k} = \frac{1}{\sqrt{\mu\varepsilon}}$

$v_p = f\lambda$

由公式易知，相速仅与媒质特性有关

真空中电磁波相速为光速

媒质本征阻抗（波阻抗）：电场幅度和磁场幅度比

$\eta = \sqrt{\frac{\mu}{\varepsilon}}$

真空（空气）的本征阻抗为 $120\pi\approx377\Omega$

对于沿 $\pmb e_k$ 方向传播的均匀平面电磁波，有

$\pmb H = \frac{1}{\eta}\pmb e_k\times\pmb E$

$\pmb E = \eta\pmb H\times\pmb e_k$

$\pmb E,\pmb H,\pmb k$ 三者相互垂直，且满足右手螺旋关系

电磁波的能量密度： $w = \varepsilon E^2 = \mu H^2$

电磁波的能流密度为

$\pmb S(t) = \pmb E(t)\times\pmb H(t) = \pmb e_k\frac{1}{\eta}E_0^2\cos^2(\omega t\pm \pmb k\cdot\pmb r)$

$\pmb S_{av} = \frac{1}{2}Re[\pmb E\times\pmb H^\ast] = \frac{1}{2\eta}E_0^2\pmb k$

电场能量密度等于磁场能量密度

电场与磁场同相，电场振幅是磁场的 $\eta$ 倍

均匀平面波在无界导电媒质中的传播

导电媒质中存在欧姆损耗，电介质被极化后存在极化损耗

通常用损耗角正切表征介质损耗特性，对导电媒质有

$\tan\delta_\sigma = \frac{\sigma}{\omega\varepsilon} = \frac{|\pmb J|}{|\pmb J_d|}$

介质损耗角正切等于导电媒质中传导电流与位移电流之比

$\begin{cases}\tan\delta_\sigma \ll 1&\text{良绝缘体}\\\\\tan\delta_\sigma \approx 1&\text{普通导电媒质}\\\\\tan\delta_\sigma\gg 1&\text{良导体}\end{cases}$

媒质导电性的强弱与频率有关

由于在导电媒质中本征阻抗为复数，磁场相位滞后于电场相位 $\displaystyle{j\frac{1}{2}\arctan\frac{\sigma}{\omega\varepsilon}}$

在损耗媒质中，相速的公式为

$v_p = \frac{\omega}{\beta(\omega)}$

色散效应：相速随频率改变而改变的现象

色散波：具有色散效应的波

导电媒质中的电磁波为色散波

在导电媒质中，电场能量密度为

$w_e = \frac{\varepsilon}{2}E^2_{xm}e^{-2\alpha z}\cos^2(\omega t - \beta z)$

磁场能量密度为

$w_m = \frac{\mu}{2}\frac{E_{xm}^2}{|\eta_c|^2}e^{-2\alpha z}\cos^2(\omega t - \beta z)$

电磁波的平均能流密度为

$\pmb S_{av} = \frac{E_m^2}{2|\eta_c|}e^{-2\alpha z}\cos\varphi\pmb k(E_m为电场振幅)$

导电媒质中均匀平面波的磁场能量大于电场能量

在波的传播过程中，电场与磁场的振幅呈指数衰减

在导电媒质中，相速不仅与媒质参数有关，而且与频率有关，为色散波

磁场能量大于电场能量

在良导体中，磁场相位滞后电场相位 $\displaystyle\frac\pi 4$

在良导体中存在趋肤效应：高频电磁波只能存在于良导体的表面层内

趋肤深度 $\delta$ ：电磁波穿入良导体中，当波的幅度下降为表面处振幅的 $\displaystyle\frac{1}{e}$ 时，波在良导体中传播的距离

对于良导体： $\displaystyle\delta = \frac{\lambda}{2\pi}$

在良绝缘体中，有：

均匀平面波的衰减小
相位常数近似等于理想媒质中的相位常数
电场和磁场之间相位差比较小

电磁波的极化

基本概念

电磁波的极化：表征空间定点处电磁波电场矢量的时变规律

波的极化描述方法：在电磁波传播空间定点处，电场强度矢量的终端端点随时间变化的轨迹形状

基本形势：线极化，圆极化，椭圆极化

电场矢量的矢端方程

电磁波的极化由电场矢量的矢端方程揭示的轨迹形状来判断

以沿 $+z$ 方向传播的均匀平面波为例，有

$|\pmb E(0,t)| = \sqrt{E_{xm}^2\cos^2(\omega t + \phi_x) + E_{ym}^2\cos^2(\omega t + \phi_y)}$

电场矢端方程为

$\frac{E_x^2}{E_{xm}^2} + \frac{E_y^2}{E^2_{ym}} - \frac{2E_xE_y}{E_{xm}E_{ym}}\cos\Delta\phi = \sin^2\Delta\phi$

其中 $\Delta\phi = \phi_y - \phi_x$

矢端的时间变化规律，决定于各分量幅度和初相的大小

任意极化均可以由线极化得到

电磁波极化方式的判断

电磁波的极化状态取决于 $E_x$ 和 $E_y$ 的振幅 $E_{xm},E_{ym}$ 和相位差 $\Delta\varphi = \varphi_y - \varphi_x$

对于沿 $+z$ 方向传播的均匀平面波：

线极化 $\Delta\varphi = 0(1,3象限),\pm\pi(2,4象限)$
圆极化 $\Delta\varphi = \pm\pi / 2,E_{xm} = E_{ym}$ ，取 $+$ 则为左旋圆极化，取 $-$ 则为右旋圆极化
椭圆极化其他情况 $0 < \Delta\varphi < \pi$ ，左旋； $-\pi < \Delta\varphi < 0$ ，右旋

任何一个线极化波、圆极化波或椭圆极化波可分解成两个线极化波的叠加

任何一个线极化波都可以表示成旋向相反、振幅相等的两圆极化波的叠加

任何一个椭圆极化波也可以表示成旋向相反、振幅不等的两圆极化波的叠加