LTI系统
基本信号分类
基本连续时间信号
-
指数信号
x(t)=Ceat
特殊形式:x(t)=ejω0t
-
正弦信号
x(t)=Acos(ω0+ϕ)
-
单位冲激信号
⎩⎨⎧δ(t)={0,t=0∞,t=0∫−∞∞δ(t)dt=1
-
单位阶跃信号
u(t)={0,t<01,t>0
基本离散时间信号
-
指数序列
x[n]=Can
特殊形式:x[n]=ejω0t
-
正弦序列
x[n]=Acos(ω0n+ϕ)
-
单位脉冲序列
δ[n]={0,n=01,n=0
-
单位阶跃序列
u[n]={0,n<01,n≥0
信号的基本变换
-
时移
x(t)→x(t−t0)
-
尺度变换
x(t)→x(at)
-
反褶
x(t)=x(−t)
信号的反褶是特殊的尺度变换,若a<0且a=−1,则信号 x(at) 是由信号x(t)同时进行尺度变换和反褶得到的
信号的性质
线性
- 齐次性
若x(t)→y(t),则kx(t)→ky(t)
- 可加性
若x1(t)→y1(t),x2(t)→y2(t),则k1x1(t)+k2x2(t)=k1y1(t)+k2y2(t)
时不变性
若x(t)→y(t),则x(t−t0)→y(t−t0)
因果性
因果性是指系统的响应不出现在激励之前(只对自变量为时间的系统有意义)
即若x(t)=0,t<t0,则y(t)=0,t<t0
稳定性
稳定系是指对于有界的激励,系统的零状态响应也是有界的
即若∣x(t∣<∞,则∣y(t)∣<∞
总而言之,LTI系统有以下特性
若x1(t)→y1(t),x2(t)→y2(t),则有k1x1(t−t1)+k2x2(t−t2)→k1y1(t−t1)+k2t2(t−t2)
信号的奇偶分量
偶信号: x(t)=x(−t)
奇信号: x(t)=−x(−t)
任何信号都可被分解为一个奇信号和一个偶信号
奇信号:Od{x(t)}=1/2[x(t)−x(−t)]
偶信号:Ev{x(t)}=1/2[x(t)+x(−t)]
离散时间LTI系统
离散时间LTI系统对于任意序列x[n]的响应为y[n]=∑k=−∞∞x[k]h[n−k],其中h[t]为单位冲激响应
连续时间LTI系统
连续时间LTI系统对于任意序列x[n]的响应为y(t)=∫−∞∞x(τ)h(t−τ)dτ
卷积的性质
-
交换律
x(t)∗h(t)=h(t)∗x(t)
-
分配律
x(t)∗[h1(t)+h2(t)]=x(t)∗h1(t)+x(t)∗h2(t)
-
结合律
x(t)∗[h1(t)∗h2(t)]=[x(t)∗h1(t)]∗h2(t)
- 求导
x′(t)∗h(t)=x(t)∗h′(t)
- 延时叠加性
x(t−t1)∗h(t−t2)=y(t−t1−t2)
LTI系统的性质
有记忆和无记忆性
若一个系统在任何时刻的输出仅与同一时刻的输入值有关,它就是无记忆的,反之则是有记忆的
可逆性
对于一个LTI系统,仅当存在一个逆系统,其与原系统级联后所产生的输出等于第一个系统的输入时,这个系统才是可逆的
给定一个LTI系统,其冲激响应为h(t),逆系统的冲激响应为h1(t),则有h(t)∗h1(t)=δ(t)
因果性
系统的因果性就是在输入事件发生之前,因果系统不会产生任何响应,这等价于初始松弛条件
因果性和初始松弛条件的等价性仅适合LTI系统
稳定性
如果一个系统对于每一个有界的输入,输出都能是有界的,则可以说明该系统是稳定的
LTI系统稳定的充要条件是单位冲激响应绝对可积(和)
∫−∞∞∣h(τ)∣dτ<∞
k=−∞∑∞∣h(k)∣<∞
单位阶跃响应
一个LTI系统的单位阶跃响应是单位冲激响应的积分(求和)
根据线性和时不变性易证
反之,我们也可以说一个LTI系统的单位冲激响应是单位阶跃响应的一阶导数(一阶差分)
用微分方程描述LTI系统
一个N阶常系数微分方程可以表示为
k=0∑Nakdtkdky(t)=k=0∑Mbkdtkdkx(t)
对于一个给定的x(t),方程的完全解为
y(t)=yp(t)+yh(t)
其中yp(t)是特解,yh(t)是齐次解
此处不赘述解微分方程的方法
上述微分方程只涉及三种基本运算:相加,乘以系数和微分,所以一个连续时间LTI系统可以通过三种基本单元:相加器,标量乘法器和微分器(常用积分器替代)的互联来表示
用差分方程描述LTI系统
一个N阶常系数的差分方程可表示为
k=0∑Naky[n−k]=k=0∑Mbkx[n−k],ak,bk为实常数
如果上述差分方程描述的系统是初始松弛的,则该系统是因果的
可以通过将差分方程写成以下形式来方便求解
y[n]=a01{k=0∑Mbkδ[n−k]−k=1∑Nakh[n−k]}
上述差分方程也只涉及到三种基本运算:相加,乘以系数和延迟,所以一个离散时间LTI系统可以通过三种基本单元:相加器,标量乘法器和单位延迟器的互联来表示
奇异函数
单位冲激信号的基本特性
∫−∞∞x(t)δ(t−t0)dt=∫−∞∞x(t+t0)δ(t)dt=x(t0)
∫baφ(t)δ(t)dt=⎩⎨⎧φ(0),ab<00,ab>0无定义,ab=0
x(t)∗δ(t−t0)=x(t−t0)
δ(t−t1)∗δ(t−t2)=δ(t−t1−t2)
单位冲激偶及其特性
单位冲激偶的符号表示是δ′(t)
有定义如下
uk(t)=(k−1)!tk−1u(t)
有时候我们也会利用以下等式表示单位冲激和单位阶跃信号
δ(t)=u0(t)
u(t)=u−1(t)
有如下定理
u−k(t)=k次u(t)∗u(t)∗⋯∗u(t)
uk(t)∗ur(t)=uk+r(t)
周期信号的傅里叶级数
LTI系统对复指数信号的响应
对于LTI系统,当输入为x(t)=est时,输出为
y(t)=H(s)est
其中H(s)为复振幅因子,和单位冲激响应的关系可表示为
H(s)=∫−∞∞h(τ)e−sτdτ
或者是
H(s)=−∞∑∞h[k]z−k
如果系统对于一个信号的输出响应仅仅是一个常数乘以输入,则称该信号为系统的特征函数,而幅度因子则称为系统的特征值
连续时间周期信号的傅里叶级数表示
对于周期为T的信号x(t),可以被分解为
x(t)=k=−∞∑∞akejkω0t=k=−∞∑∞akejkT2πt
其中ak被称为x(t)的频谱系数,可以通过下列式子求出
ak=T1∫Tx(t)e−jkω0tdt=T1∫Tx(t)e−jkT2πtdt
当k=0时,求取的值为x(t)的一个周期的平均值(直流分量)
使用傅里叶级数的前提是满足Dirichlet条件,即
-
在任何周期内,x(t)都绝对可积
-
在任何有限区间内,x(t)都具有有限个最大值和最小值
-
在任何有限区间内,x(t)都具有有限个不连续点,并且每个不连续点都为有限值(即有限个第一类间断点)
Dirichlet条件只是充分条件,而非必要条件
也有三角型傅里叶级数的表示方法
x(t)=a0+2k=1∑∞(Bkcoskω0t−Cksinkω0t)
其中,Bk,Ck和频谱系数的关系是ak=Bk+jCk
也可以表示为谐波类型的级数
x(t)=a0+2k=1∑∞Akcos(kω0t+θk)
其中Ak,θk与频谱系数的关系为ak=Akejθk
连续时间傅里叶级数的性质
若x(t)⟷FSak,y(t)⟷FSbk
线性
z(t)=Ax(t)+By(t)⟷FSck=Aak+Bbk
时移性质
x(t−t0)⟷FSbk=e−jkω0t0ak
时间反转
x(−t)⟷FSa−k
尺度变换
若有
x(t)=k=−∞∑∞akejkω0t
则有
x(at)=k=−∞∑∞akejk(aω0)t
相乘
x(t)y(t)⟷FShk=l=−∞∑∞albk−l
共轭对称性
x∗(t)⟷FSa−k∗
⎩⎨⎧x(t)=x∗(t)⟹ak=a−k∗,∣ak∣=∣a−k∣,Ev{x(t)}⟷FSRe{ak},Od{x(t)}⟷FSjIm{ak}x(t)=x∗(t),x(t)=x(−t)⟹ak=a−k,ak=ak∗x(t)=x∗(t),x(t)=−x(−t)⟹a0=0,a−k=−ak,a−k=ak∗
帕斯瓦尔定理
T1∫T∣x(t)∣2dt=k=−∞∑∞∣ak∣2
离散时间傅里叶级数的表示
对于一个基波周期为N的周期序列x[n]而言,离散傅里叶级数可以表示为
x[n]=k=<N>∑x[n]e−jkω0n
其中k=<N>的意思是从任意k值开始向后算N个数字(即离散序列的一个周期)
由于离散傅里叶级数的项是有限的,所以不需要考虑收敛问题
离散傅里叶级数性质
周期性,线性,时间反转,共轭对称,相乘和帕斯瓦尔定理不赘述,和连续时间基本一致
若有x[n]⟷FSak,y[n]⟷FSbk
时移性质
x[n−n0]⟷FSbk=ake−jkω0n0,∣bk∣=∣ak∣
频移性质
ejMN2πnx[n]⟷FSak−M
时域尺度变换
x(m)[n]=⎩⎨⎧x[mn],n是m的倍数0,n不是m的倍数⟷FSm1ak
其中x(m)(t)和m1ak的周期均为mN
周期卷积
r=<N>∑x[r]y[n−r]⟷FSNakbk
频域相乘 ⟺ 时域相卷,频域相卷 ⟺ 时域相乘
一阶差分
x[n]−x[n−1]⟷FS(1−e−jkN2π)ak
求和
k=−∞∑nx[k]⟷FS1−e−jkN2πak
傅里叶级数与LTI系统
当s为一般复数时,H(s)称为该系统的系统函数;当s=jω时,H(s)=H(jω),此时的系统函数称为该系统的频率响应
H(jω)=∫−∞∞h(t)e−jωtdt
H(ejω)=n=−∞∑∞h[n]e−jωn
对于可以被分解为傅里叶级数的周期信号(无论连续还是离散),其LTI系统的响应都可以被分解为如下形式
y(t)=k=−∞∑∞akH(ejkω0)ejkω0t
y[n]=k=<N>∑akH(ejkNwπn)ejkN2πn
连续时间傅里叶变换
傅里叶变换
傅里叶变换
X(jω)=F{x(t)}=∫−∞∞x(t)e−jωtdt
逆傅里叶变换
x(t)=F−1{X(jω)}=2π1∫−∞∞X(jω)ejωtdω
一个非周期信号x(t)的傅里叶变换X(jω)被称为信号的频谱,一般情况下,可表示为如下形式
X(jω)=∣X(jω)∣ejφ(ω)
其中∣X(jω)∣称为幅度谱,φ(t)被称为相位谱
傅里叶变换收敛的条件也和傅里叶级数一样
连续时间傅里叶变换的性质
线性,时移,频移,共轭对称性质和帕斯瓦尔定理不做赘述,和傅里叶级数基本一致
若有x(t)⟷FTX(jω),x1(t)⟷FTX1(jω)x2(t)⟷FTX2(jω)
时域微分积分性质
dtdx(t)⟷FTjωX(jω)
∫−∞tx(τ)dτ⟷FTjω1X(jω)+πX(0)δ(ω)
频域微分积分性质
(−jt)x(t)⟷FTdωdX(jω)
−jt1x(t)+πx(0)δ(t)⟷FT∫−∞∞X(jΩ)dΩ
尺度变换
x(at)⟷FT∣a∣1X(ajω)
对偶性
X(jt)⟷FT2πx(−ω)
卷积相乘性
x1(t)∗x2(t)⟷FTX1(jω)X2(jω)
x1(t)x2(t)⟷FT2π1[X1(jω)∗X2(jω)]
连续时间LTI系统的频率响应
频率响应函数
一个连续时间LTI系统的输出可以表示为
y(t)=x(t)∗h(t)
根据卷积相乘性可得
Y(jω)=X(jω)H(jω)⟹H(jω)=X(jω)Y(jω)
其中,H(jω)称为系统的频率响应函数
H(jω)=∣H(jω)∣ejφH(ω)
∣H(jω)∣称为系统的幅频响应,φH(ω)称为系统的相频响应
只有稳定系统才存在频率响应
若LTI系统满足以下的线性常系数微分方程
k=0∑Nakdtkdky(t)=k=0∑Mbkdtkdkx(t)
则该系统的频率响应为
H(jω)=∑k=0Nak(jω)k∑k=0Mbk(jω)k
无失真传输
一个确定的信号经过系统之后,时域波形无改变,仅幅度产生变换,时间上有所延迟
即输出为
y(t)=Kx(t−td)
易得无失真系统必须满足以下条件
∣H(jω)∣=K,φH(ω)=−ωtd
也就是说幅频响应必须是一个和频率无关的常数,相频响应必须是频率的线性函数(群延迟)
滤波
频率成形滤波器
用于改变频谱的形状的LTI系统,常见的有微分滤波器,常用于图像边缘的增晰
频率选择性滤波器
- 理想低通滤波器
H(jω)=⎩⎨⎧1,∣ω∣<ωc0,∣ω∣>ωc
-
理想高通滤波器
H(jω)=⎩⎨⎧0,∣ω∣<ωc1,∣ω∣>ωc
-
理想带通滤波器
H(jω)=⎩⎨⎧1,ωc1<∣ω∣<ωc20,else
-
理想带阻滤波器
H(jω)=⎩⎨⎧0,ωc1<∣ω∣<ωc21,else
带宽
滤波器带宽
理想低通滤波器的绝对带宽是它的截止频率,称为绝对带宽
理想带通滤波器的绝对带宽是ωc2−ωc1
高通和带阻滤波器没有带宽的定义
而对于实际的滤波器,常见的带宽定义是3dB带宽
一般是指幅度谱H(jω)下降3dB的宽度
信号带宽
信号也有3dB带宽,也有有限带宽信号,即∣X(jω)∣=0,∣ω∣>ωm,则为有限带宽信号,带宽为ωm
离散时间傅里叶变换
信号与系统不考,暂略,等我学完DSP再补教程
信号与系统的时域和频域特性
傅里叶变换的模和相位表示
一般而言,傅里叶变换之后的结果是复数,并且可以通过它的实部和虚部来得到模和相位的一些信息
对于连续时间傅里叶变换X(jω)的模-相表示为
X(jω)=∣X(jω)∣ej∢X(jω)
同理,对于离散时间傅里叶变换X(jω)表示为
X(ejω)=∣X(ejω)∣ej∢X(ejω)
从傅里叶变换的公式本身来看,X(jω)本身可以看作是信号x(t)的一种分解,即分解为许多不同频率的复指数信号之和
其中,∣X(jω)∣表示各个频率复指数信号的相对的振幅信息,∢X(jω)表示的是各个频率分量的相对相位信息
LTI系统频率响应的模和相位表示
由傅里叶变换的卷积性质我们可以得出,LTI系统输入和输出的傅里叶变换X(jω)和Y(jω)是由如下关系联系起来的
Y(jω)=H(jω)X(jω)
而对于离散时间情况下,有
Y(ejω)=H(ejω)X(ejω)
而我们从模-相关系去看待这些关系式,不难得出以下结论
∣Y(jω)∣=∣H(jω)∣∣X(jω)∣
∢Y(jω)=∢H(jω)+∢X(jω)
而在离散时间系统下,也有相似的结论
至此,我们可以归纳一下,LTI系统对于输入信号的作用就是增益和相移
当系统对于输入信号的幅度和相位的改变不符合我们的预期,那么这种现象就称为幅度/相位失真
线性与非线性相位
当相移是ω的线性函数时,就有
∢H(jω)=−ωt0
从而有时移的效果
y(t)=x(t−t0)
当相移不是线性函数时,在输入当中各个不同频率的复指数分量都会移位,它们的相对相移会产生很大的变化,从而导致叠加之后的信号看上去和输入信号有很大的不同
群延迟
设想我们需要检查一个连续时间LTI系统的相移对一个窄带输入信号产生的效果
该窄带信号的傅里叶变换在除了ω=ω0为中心的很小一个频率范围之外的都是0或者极小,如果将这个频带取得足够小,则可以将这个系统的相位特性准确的用线性关系来近似
∢H(jω)≃−ϕ−ωα
也就可以得到
Y(jω)≃X(jω)∣H(jω)∣e−jϕe−jωα
于是可以说在以ω=ω0为中心的很小的一个频带上面的延迟为α秒,即在ω=ω0的群延迟
在每个频率上的群延迟等于在那个频率上相位特性斜率的负值
τ(ω)=−dωd{∢H(jω)}
群延迟的概念也适用于离散时间系统当中
伯德图
为了方便观察,一般会使用伯德图来描绘信号的幅频特性
伯德图的一般是采用对数为坐标的,即20log10为单位,称为分贝
则易知,0dB对应无增益,频率响应的模为1;20dB对应10倍增益;-20dB对应10倍减益
伯德图有两部分,分别是幅值图和相位图
图的横坐标都是对数频率坐标,优点是可以非常直观的看到较大范围的频率的特性
非理想滤波器
很多情况下我们做不到理想滤波器的效果,所以我们还需要对非理想滤波器进行分析
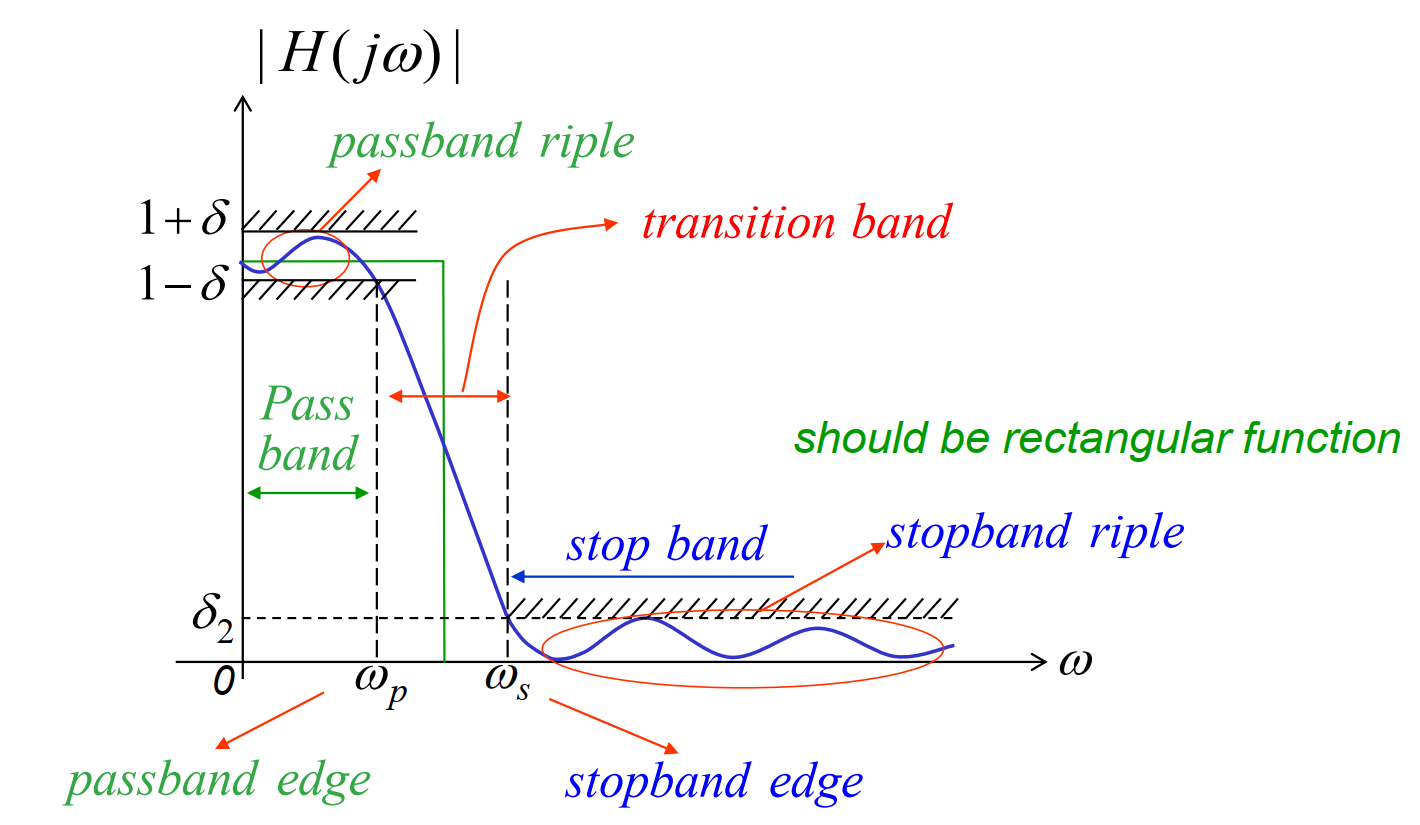
如图所示,这是一个连续时间低通滤波器
我们会对偏离单位增益的±δ进行限制,也就是可容许的通带偏离
而δ2就是可容许的阻带偏离
这两个量分别被称为通带起伏和阻带起伏
ωp和ωs分别称为通带边缘和阻带边缘
从ωp到ωs的那一段被称为过渡带
采样
冲激串采样
对于一个连续信号x(t),若用冲激串p(t)=∑n=−∞∞δ(t−nT)对其进行采样,则时域结果为
xp(t)=x(t)⋅p(t)
在频域内则有
Xp(jω)=T1k=−∞∑∞X(j(ω−kωs))
ωs=T2π
采样定理
设x(t)是一个带限信号,在∣ω∣>ωM时,X(jω)=0,如果采样频率大于原信号频率的两倍ωs>2ωM,那么x(t)就可以被样本唯一的还原(重建)出来
利用内插由采样点重建信号
如果在采样过程中没有出现频谱的混叠现象,则可以让xp(t)通过一个截止频率为ωc=2ωs的理想低通滤波器,就可以无失真的恢复原始信号
内插公式如下所示
xr(t)=∑x(nT)πωcT⋅ωc(t−nT)sin[ωc(t−nT)]
其中ωc=2ωs
拉普拉斯变换
定义
对于连续时间信号x(t),其双边拉普拉斯变换定义为
X(s)=∫−∞∞x(t)e−stdt
其中
s=σ+jω
若σ=0,则复平面的虚轴上的拉普拉斯变换就是连续时间的傅里叶变换
收敛域
能够使∫−∞∞x(t)e−stdt收敛的所有s值的集合,称为拉普拉斯变换的收敛域
-
绝对可积的信号的收敛域为整个s平面
-
右边信号的收敛域是s平面的某个右半平面
-
左边信号的收敛域是s平面的某个左半平面
-
双边信号的收敛域可能是一个平行于虚轴的带状区域,也可能收敛域不存在
拉普拉斯变换还包括以下一些性质
- 收敛域不包含极点(可以包含零点)
- 如果拉普拉斯变换X(s)是有理数,则收敛域的边界可以由极点确定
拉普拉斯逆变换
进行逆变换时,通常先根据收敛域判断x(t)的类型,然后再进行计算
通常我们使用部分分式展开法
先将X(s)展开为
X(s)=i=1∑ms+aiAi
然后利用变换对
Aie−aitu(t)⟷LTs+aiAi
对每一项进行逆变换,就可以得到x(t)了
拉普拉斯变换的性质
设x(t)⟷LTX(s),ROC=R;x1(t)⟷LTX1(s),ROC=R1;x2(t)⟷LTX2(s),ROC=R2
线性
ax1(t)+bx2(t)⟷LTaX1(s)+bX2(s),ROC包含R1∩R2
时移频移性
x(t−t0)⟷LTe−st0X(s),ROC=R
es0tx(t)⟷LTX(s−s0),ROC=R+Re{s0}
尺度变换
x(at)⟷LT∣a∣1X(as),ROC=aR
共轭性质
x∗(t)⟷LTX∗(s∗),ROC=R
时域卷积性质
x1(t)∗x2(t)⟷LTX1(s)⋅X2(s),ROC包含R1∩R2
时域积分微分性质
∫−∞tx(τ)dτ⟷LTsX(s),ROC包含R∩{Re{s}>0}
dtdx(t)⟷LTsX(s),ROC包含R
s域微分性质
−tx(t)⟷LTdsdX(s),ROC=R
初值定理
设x(t)是因果信号,则有x(0+)=s→∞limX(s)
终值定理
若X(s)的所有极点要么位于s左半平面,要么是位于原点的一阶极点,则有t→∞limx(t)=s→0limX(s)
拉普拉斯变换的系统函数
定义和傅里叶变换部分的系统函数基本相同
H(s)=L{h(t)}=∫−∞∞h(t)e−stdt
对于一个具有有理系统函数的LTI系统而言,其因果性⟺ROC在H(s)最右边极点的右半平面
如果没有有理的系统函数,那就是反之不然的
一个连续的LTI系统是稳定的⟺系统函数H(s)的ROC包含jω轴
单边拉普拉斯变换
X(s)=∫0−∞x(t)e−stdt
一个因果信号的单边拉普拉斯变换的结果和双边拉普拉斯变换相同
信号x(t)的单边拉普拉斯变换等于信号x(t)u(t)的双边拉普拉斯变换
单边拉普拉斯变换的性质
下面仅列出和双边拉普拉斯变换不同的性质
设x(t)⟷LTX(s),x1(t)⟷LTX1(s),x2(t)⟷LTX2(s)
时域卷积
x1(t)∗x2(t)⟷LTX1(s)⋅X2(s)
其中x1(t),x2(t)必须为因果信号
时域微分积分
dtndnx(t)⟷LTsnX(s)−k=0∑n−1sn−k−1x(k)(0−)
∫0−tx(τ)dτ⟷LTs1X(s),此处x(t)必须为因果信号
尺度变换
x(at)⟷LTa1X(as),a>0
z变换
定义
对于序列x[n],其双边z变换定义为
X(z)=n=−∞∑∞x[n]z−n
z=rejω
若r=1,则在单位圆上进行的z变换就是离散时间傅里叶变换
收敛域
能使洛朗级数∑n=−∞∞x[n]z−n收敛的z的集合称为z变换的收敛域
收敛域有以下几种类型
-
有限长序列的收敛域为整个z平面
-
右边序列的收敛域是某个圆的外部区域
-
左边序列的收敛域是某个圆的内部区域
-
双边序列的收敛域是夹在两个半径有限的圆的环形区域,或者不存在
收敛域还有以下一些性质
- 收敛域不包含极点
- 若z变换X(z)是有理函数,则其收敛域的边界由其极点确定
- 若x[n]为因果序列(当n<0时,x[n]=0),X(z)的收敛域将包含z=∞
- 若x[n]为反因果序列(当n>0时,x[n]=0),X(z)的收敛域将包含z=0
逆z变换
在进行逆z变换时,应该先通过ROC判断x[n]类型,然后选用合适的方法进行计算
幂级数展开法
若X(z)为有理函数,则可以通过长除法将X(z)展开成幂级数,取各项的系数就可以得到x[n]
部分分式展开法
可以先将有理的X(z)展开为
X(z)=i=1∑m1−aiz−1Ai=i=1∑mz−aiAiz
然后利用变换对
Aiainu[n]⟷ZT1−aiz−11
对以上和式的每一项求逆变换,就可以得到x[n]
z变换的性质
设x[n]⟷ZTX(z),ROC=R;x1[n]⟷ZTX1(z),ROC=R1;x2[n]⟷ZTX2(z),ROC=R2
线性
ax1[n]+bx2[n]⟷ZTaX1(z)+bX2(z),ROC包含R1∩R2
时移性
x[n−n0]⟷ZTz−n0X(z),ROC=R
z=0或z=∞可能加入R当中,或者被剔除出去
尺度变换
z0nx[n]⟷ZTX(z0z),ROC=∣z0∣R
时域扩展
若定义
x(k)[n]=⎩⎨⎧x[kn],n为k的倍数0,n不为k的倍数
则有
xk[n]⟷ZTX(zk),ROC=kR
共轭性质
x∗[n]⟷ZTX∗(z∗),ROC=R
时域卷积性质
x1[n]∗x2[n]⟷ZTX1(z)⋅X2(z),ROC包含R1∩R2
z域微分
nx[n]⟷ZT−zdzdX(z),ROC=R
初值定理
设x[n]为因果序列,即当n<0时,x[n]=0,则有
x[0]=z→∞limX(z)
终值定理
若x[n]为因果序列,则有
n→∞limx[n]=z→1lim(z−1)X(z)
z变换的系统函数
定义和傅里叶变换部分的系统函数基本相同
H(z)=Z{h[n]}=n=−∞∑∞h[n]z−n
若某离散LTI系统的系统函数H(z)的收敛域是某个圆的外部区域,并且包含z=∞,则该系统是因果的;反之亦然
一个离散LTI系统是稳定的⟺系统函数H(z)的ROC包含单位圆∣z∣=1
单边z变换
对于序列x[n],其单边z变换定义为
Z(z)=n=0∑∞x[n]z−n
一个因果序列的单边z变换和双边z变换相同
序列x[n]的单边z变换等于序列x[n]u[n]的双边z变换
单边z变换的性质
这里仅列出和双边z变换不同的性质
设x[n]⟷ZTZ(z),x1[n]⟷ZTZ1(z),x2[n]⟷ZTZ2(z)
时域卷积性质
x1[n]∗x2[n]⟷ZTZ1(z)⋅Z2(z)
其中x1[n],x2[n]必须均为因果序列
累加和性质
k=0∑nx[k]⟷ZT1−z−11Z(z)
此处x[n]必须是因果序列
时域延时和超前
x[n−m]⟷ZTz−m[Z(z)+∑n=−1−mx[n]z−n],m>0
x[n+m]⟷ZTz−m[Z(z)−∑n=0m−1x[n]z−n],m>0
至于通信系统下次再补谔谔,我手都要断了😭
现在是,摸🐟时间


