导论

存储格式

数字化后的图像数据在计算机中一般有两种存储方式，一种是位图模式，而另一种是矢量图模式

位图又称点阵图，是将图像的每一点数值存放在以字节为单位的矩阵中

矢量图不存储图像数据的每一点，而是存储图像内容的轮廓部分

色彩存储

  1. RGB

我们最熟悉的色彩表现方式就是以红绿蓝三原色为基色的RGB

颜色 R G B
红 255 0 0
绿 0 255 0
蓝 0 0 255
黄 255 255 0
紫 255 0 255
青 0 255 255
白 255 255 255
黑 0 0 0
灰 128 128 128
  1. BGR

其实就是RGB颠倒了一下，区别不大，但是OpenCV库当中常常使用BGR（历史遗留问题）

  1. CMYK

CMYK中的每个字母代表一种颜色（青、品红、黄、黑），每个数字的取值范围为00~100%100\%，百分比越高，说明颜色中含有这种原色的比例越高，常用于平面印刷

分辨率

  1. 图像的空间分辨率

图像的空间分辨率是指图像中每单位长度所包含的像素或点的数目，常以像素/英寸（pixels per inch，ppi）为单位来表示

如72ppi表示图像中每英寸包含72个像素或点

  1. 图像的灰度级/辐射计量分辨率

灰度级分辨率又称色阶，是指图像中可分辨的灰度级的数目

由于灰度级度量的是投射到传感器上的光辐射值的强度，所以灰度级分辨率又称为辐射计量分辨率

像素关系

对于坐标分别为(x,y),(s,t)(x,y),(s,t)和(v,w)(v,w)的像素p,q,zp,q,z，不妨设DD为两个像素之间的距离，则有

  1. D(p,q)≥0(当且仅当p=q时取等)D(p,q)\ge0(当且仅当p=q时取等)
  2. D(p,q)=D(q,p)D(p,q) = D(q,p)
  3. D(p,z)≤D(q,p)+D(q,z)D(p,z)\le D(q,p)+D(q,z)

像素的距离不止一种，其定义式如下

  1. 欧氏距离

De(p,q)=[(x−s)2+(y−t)2]12D_e(p,q) = [(x-s)^2 + (y-t)^2]^{\frac 12}

  1. 街区距离

D4(p,q)=∣x−s∣+∣y−t∣D_4(p,q) = |x-s| + |y-t|

  1. 棋盘距离

D8(p,q)=max⁡(∣x−s∣,∣y−t∣)D_8(p,q) = \max(|x-s|,|y-t|)

图像增强

直接灰度映射

灰度映射分为线性变换和非线性变换两种类型

线性变换

设输入图像的灰度取值区间为f(m,n)∈[a,b]f(m,n)\in[a,b]，线性变换之后输出为g(m,n)∈[c,d]g(m,n)\in[c,d]，变换过程的表达式为

g(m,n)=c+k[f(m,n)−a]g(m,n) = c + k[f(m,n) - a]

其中k=d−cb−ak = \frac{d-c}{b-a}，称为变换函数的斜率

除了普通的一次函数的变换函数之外，也有分段线性变换函数

非线性变换

常用的非线性变换方法主要是指数变换和对数变换

对数变换的表达式为

g(m,n)=λlog⁡(1+f(m,n))g(m,n) = \lambda\log(1+f(m,n))

其中λ\lambda为一个调节常数，用它来调节变换后的灰度值，使其符合实际要求

对数变换的作用是扩展图像的低灰度范围，同时压缩高灰度范围，使得图像的灰度分布均匀

与对数变换的效果相反，指数变换的作用在于扩展高灰度范围的同时压缩低灰度范围，其一般表达形式为

g(m,n)=λ(f(m,n)+ε)γg(m,n) = \lambda(f(m,n) + \varepsilon)^\gamma

其中λ\lambda和γ\gamma为常数，为了避免出现底数为0的情况，引入了偏移量ε\varepsilon

当γ<1\gamma<1时，变换过程将图像的灰度向高亮度的部分映射

当γ>1\gamma>1时，变换过程将图像的灰度向低亮度的部分映射

直方图变换

灰度直方图

灰度直方图定义为数字图像中各灰度级与其出现的频数（次数）间的统计关系，可表示为

P(k)=nkn, k=0,1,⋯ ,L−1P(k) = \frac{n_k}n,~k = 0,1,\cdots,L-1

且∑k=0L−1P(k)=1\displaystyle{\sum^{L-1}_{k=0}P(k) = 1}，其中，kk为图像的灰度级，nkn_k为灰度级kk在图像中出现的总次数，nn为图像的像素总数，LL为灰度级的数目

灰度直方图（histogram） 是灰度级的函数，它表示图象中具有每种灰度级的像素的个数，反映图像中每种灰度出现的频率，是图像的最基本的统计特征

直方图均衡化

直方图均衡化主要用于增强动态范围较小的图像的灰度反差，该方法的基本思想是把原始图像的直方图变换为均匀分布的形式，这样就增加了像素灰度值的动态范围，从而达到增强图像整体对比度的目的

能够使直方图实现均匀分布的灰度变换函数需同时满足如下的两个条件：

  1. s=T(r)s = T(r)在区间0≤r≤10\le r\le1（归一化后的灰度取值范围）内是单调递增函数
  2. rr与T(r)T(r)的取值范围一致，即当0≤r≤10\le r\le 1时，0≤s=T(r)≤10\le s = T(r)\le1

同时，其反函数r=T−1(s)r = T^{-1}(s)也应满足这两个条件

直方图均衡化计算步骤如下：

  1. 列出输入图像和输出图像的灰度级：i,j=0,1,2,⋯ ,L−1i,j = 0,1,2,\cdots,L-1，其中LL是灰度级的总数
  2. 统计输入图像中的各灰度级出现的次数（像素个数）nin_i
  3. 计算输入图像的直方图：P(i)=ninP(i) = \frac{n_i}n，其中nn为输入图像的像素总数
  4. 计算输入图像的累积直方图：Pj=∑k=0jP(k)\displaystyle{P_j = \sum^j_{k=0}P(k)}
  5. 利用上一步所示的灰度变换函数计算输出图像的各灰度值，并按照如下的方式进行取整：j=INT[(L−1)Pj+0.5]j = INT[(L-1)P_j + 0.5]
  6. 按照如下的方式对灰度进行修正：i→ji\rightarrow j
  7. 统计输出图像中的各灰度级出现的次数（像素个数）njn_j
  8. 计算输出图像的直方图：P(j)=njnP(j) = \frac{n_j}n

变换后图像的灰度级的出现次数并不是严格均匀的，因为由于数字图像灰度取值的离散性，导致经由四舍五入操作后的灰度值出现了归并现象

因此，变换后的直方图并非完全均匀分布，但相比于原直方图要平坦得多

直方图规定化

直方图均衡化的优点是能自动地增强整个图像的对比度，但它
的具体增强效果却不易控制，处理的结果总是得到全局优化的
直方图

实际中有时需要变换直方图使之成为某个需要的形状，从而有选择地增强某个灰度值范围内的对比度或使图像灰度值的分布满足特定的要求

这时可以采用比较灵活的直方图规定化方法

例如：

  • 正态扩展
  • 均匀化
  • 暗区扩展
  • 亮区扩展

其计算步骤如下：

  1. 对原始图像执行直方图均衡化操作，即Pi=∑k=0iPr(k),i=0,1,2,⋯ ,L−1P_i = \sum^i_{k=0}P_r(k),i = 0,1,2,\cdots,L-1
  2. 对规定直方图执行均衡化操作，即Pj=∑l=0jPr(l),j=0,1,2,⋯ ,L−1P_j = \sum^j_{l=0}P_r(l),j = 0,1,2,\cdots,L-1
  3. 按照Pj→PiP_j\rightarrow P_i最靠近的原则进行i→ji\rightarrow j的变换
  4. 求出i→ji\rightarrow j的变换函数，最后，对原始图像进行灰度变换j=T[i]j = T[i]即可

空域滤波

领域平均法

即用当前运算点所在邻域的灰度平均值来代替该点的灰度值

g(m,n)=favg=1N∑(i,j)∈Sf(i,j)g(m,n) = f_{avg} = \frac 1N \sum_{(i,j)\in S}f(i,j)

常见的领域平均法有

  • 4-领域平均
  • 8-领域平均

领域平均法会使得图像中目标的轮廓或细节变得模糊

阈值平均法

为克服邻域平均的模糊效应，可以采用加门限的方法来减少这
种模糊，具体的计算公式如下

g(m,n)={favg∣f(m,n)−favg∣>Tf(m,n)elseg(m,n) = \begin{cases}f_{avg}\quad &|f(m,n)-f_{avg}|>T\\f(m,n)\quad &else\end{cases}

其中的TT通常选择为T=k+σfT = k + \sigma_f，σf\sigma_f为图像的均方差

在实际应用中，TT的选取需要借助于经验和多次尝试来获得

这种方法对抑制椒盐噪声很有效，也能较好的保护仅有微小变化的目标细节

加权平均法

即滑动窗中不同位置处的系数不再完全相同

一般认为， 离窗中心位置近的像素对滤波结果的贡献较大，所以，接近窗中心位置的系数可以取得较大，而边界附近的系数可以采用较小的数值

[⋱⋮⋮⋮⋅⋅⋅⋯较小较小较小⋯⋯较小较大较小⋯⋯较小较小较小⋯⋅⋅⋅⋮⋮⋮⋱]\left[ \begin{array}{ccccc} \ddots & \vdots & \vdots & \vdots & {\cdot^{\cdot^{\cdot}}} \\ \cdots & 较小 & 较小 & 较小 & \cdots \\ \cdots & 较小 & 较大 & 较小 & \cdots \\ \cdots & 较小 & 较小 & 较小 & \cdots \\ {\cdot^{\cdot^{\cdot}}} & \vdots & \vdots & \vdots & \ddots \end{array} \right]

非线性滤波

中值滤波

一个窗口（记为WW）内的所有像素的灰度值进行排序，取排序结果的中间值作为WW中心点处像素的输出响应值

g(m,n)=med{f(m−i,n−j),(i,j)∈W}g(m,n) = med\{f(m-i,n-j),(i,j)\in W\}

中值滤波对干扰脉冲和点噪声有着良好的抑制作用，同时，能够较好的保留图像的边缘细节

中值滤波常用的窗口形状如下

  • 线状
  • 十字状
  • XX状
  • 方形
  • 菱形
  • 圆形

中值滤波的重要特性：

  1. 对离散阶跃信号（或斜降）信号不产生影响
  2. 持续个数小于窗口宽度一半的离散脉冲将被滤除掉
  3. 三角形信号的顶部将被削平

使用中值滤波的注意事项：

  1. 中值滤波适合于滤除椒盐噪声和干扰脉冲，尤其适合于目标形状是块状时的图像滤波
  2. 具有丰富尖角几何结构的图像，一般采用十字形滤波窗口，且窗口大小最好不要超过图像中最小目标的尺寸，否则会丢失目标的细小几何特征
  3. 当需要保持细线状及尖顶角等目标细节时，最好不要采用中值滤波

空域微分法

邻域平均和加权平均皆对应于数学中的积分过程，其滤波过程的表现效果为平滑

反之，若将积分过程的反向运算形式即微分算子作用于图像之上，则滤波过程的表现效果转变为锐化

  1. 梯度法

∇f=[∂f∂x,∂f∂y]=[Gx,Gy]T\nabla f = [\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}] = [G_x,G_y]^T

在离散空间内，微分借助于差分来实现，如下是常用的两个差分模板

在实际滤波时，常采用梯度矢量的模

∣∇f(2)∣=max⁡(∇f)=[GX2+GY2]122范数|\nabla f_{(2)}| = \max(\nabla f) = [G_X^2 + G_Y^2]^{\frac 12}\quad 2范数

∣∇f(1)∣=∣GX∣+∣GY∣1范数|\nabla f_{(1)}| = |G_X| + |G_Y|\quad 1范数

∣∇f(∞)∣=max⁡{∣GX∣,∣GY∣}∞范数|\nabla f_{(\infty)}| = \max\{|G_X|,|G_Y|\}\quad \infty 范数

  1. 拉普拉斯算子法

对于离散图像，有

g(m,n)=f(m,n)+α∇2fg(m,n) = f(m,n) + \alpha\nabla^2 f

二阶微分的计算公式如下：

∂2f∂x2=f(m+1,n)+f(m−1,n)−2f(m,n)\frac{\partial^2 f}{\partial x^2} = f(m+1,n)+f(m-1,n)-2f(m,n)

∂2f∂y2=f(m,n+1)+f(m,n−1)−2f(m,n)\frac{\partial^2 f}{\partial y^2} = f(m,n+1)+f(m,n-1)-2f(m,n)

  1. 模版锐化（高通滤波）法

4-领域模版如下

W1=[0−α0−α1+4α−α0−α0]W_1 = \left[ \begin{array}{ccc} 0 & -\alpha & 0\\ -\alpha & 1+4\alpha & -\alpha\\ 0 & -\alpha & 0 \end{array} \right]

8-领域模版如下

W2=[−α−α−α−α1+8α−α−α−α−α]W_2 = \left[ \begin{array}{ccc} -\alpha & -\alpha & -\alpha\\ -\alpha & 1+8\alpha & -\alpha\\ -\alpha & -\alpha & -\alpha \end{array} \right]

对于一般图像， 处理前后其平均灰度保持不变

算法的实质是：锐化图像g(m,n)=g(m,n)=原图像f(m,n)+f(m,n)+清晰度被强化后的边缘(α×(\alpha\times微分))

频域滤波

频域增强原理

在频域空间内，图像的信息表现为不同频率分量的组合

如果能让某个范围内的分量或某些频率的分量受到抑制而让其他分量不受影响，就可以改变输出图像的频率分布，进而达到不同的增强目的

执行步骤

  1. 计算输入图像的傅里叶变换
  2. 将其与自定义的转移函数相乘
  3. 对结果执行傅里叶反变换， 此时的输出即为最终的增强图像

低通滤波

低通滤波可以消除或削弱噪声，代价是图像的边缘会变得模糊

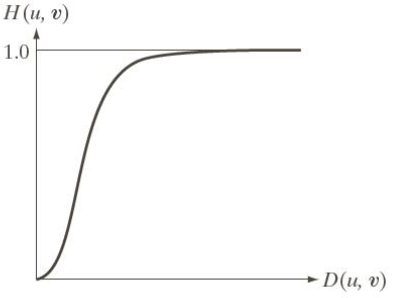
理想低通滤波器

H(u,v)={1D(u,v)≤D00D(u,v)>D0H(u,v) = \begin{cases}1\quad D(u,v)\le D_0\\0\quad D(u,v)>D_0\end{cases}

其中D(u,v)D(u,v)为点(u,v)(u,v)到频率平面原点的距离，D0D_0为截至频率

其图像如图所示

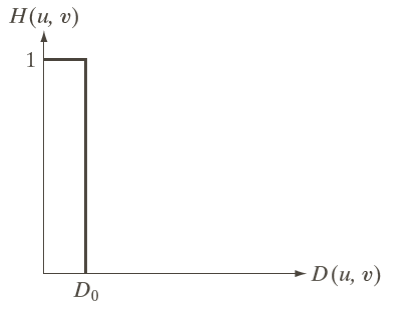
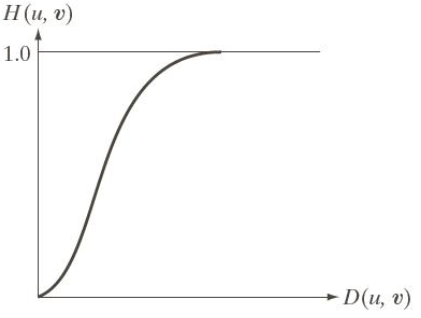
Butterworth低通滤波器（BLPF）

H(u,v)=11+[D(u,v)D0]2nH(u,v) = \frac{1}{1 + \left[\frac{D(u,v)}{D_0}\right]^{2n}}

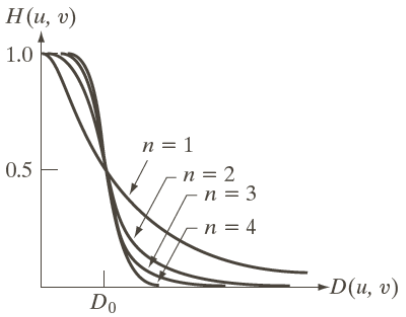
高斯低通滤波器（GLPF）

H(u,v)=exp⁡{−[D(u,v)D0]n}H(u,v) = \exp\left\{-\left[\frac{D(u,v)}{D_0}\right]^n\right\}

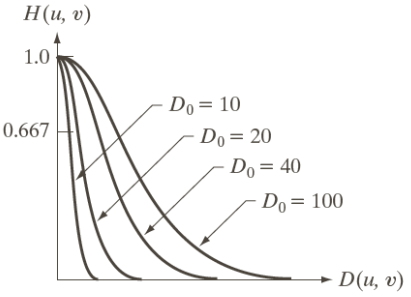
高通滤波

理想高通滤波器

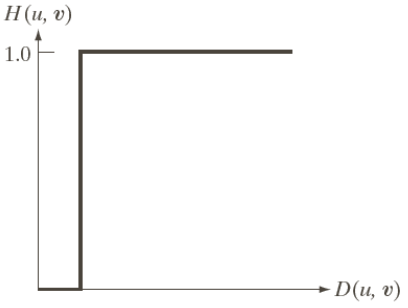
H(u,v)={0D(u,v)≤D01D(u,v)>D0H(u,v) = \begin{cases}0\quad D(u,v)\le D_0\\1\quad D(u,v)>D_0\end{cases}

Butterworth高通滤波器（BHPF）

H(u,v)=11+[D0D(u,v)]2nH(u,v) = \frac{1}{1 + \left[\frac{D_0}{D(u,v)}\right]^{2n}}

高斯高通滤波器（GHPF）

H(u,v)=1−exp⁡{−[D(u,v)D0]n}H(u,v) = 1-\exp\left\{-\left[\frac{D(u,v)}{D_0}\right]^n\right\}

图像变换

图像的几何变换

[u,v]=[X(x,y),Y(x,y)][u,v] = [X(x,y),Y(x,y)]

其中，[u,v][u,v]为变换后的图像像素的笛卡尔坐标，(x,y)(x,y)为原始图像像素的笛卡尔坐标

此处简单的变换不做赘述，仅简要列出变换种类

  1. 平移
  2. 比例缩放
  3. 旋转

仿射变换

平移、比例缩放和旋转变换皆为仿射变换的特殊情形

[uv]=[a2a1a0b2b1b0][xy1]\left[ \begin{array}{c} u\\v \end{array} \right] = \left[ \begin{array}{ccc} a_2 & a_1 & a_0\\b_2 & b_1 & b_0 \end{array} \right] \left[ \begin{array}{c} x\\y\\1 \end{array} \right]

透视变换

透视变换(Perspective Transformation)是指将图像投影到一个新的视平面(Viewing Plane)上的变换过程，也称作投影映射(Projective Mapping)

通用的变换公式为

[u′v′w′]=[a11a12a13a21a22a23a31a32a33][xy1]\left[ \begin{array}{c} u'\\v'\\w' \end{array} \right] = \left[ \begin{array}{ccc} a_{11} & a_{12} & a_{13}\\a_{21} & a_{22} & a_{23}\\a_{31} & a_{32} & a_{33} \end{array} \right] \left[ \begin{array}{c} x\\y\\1 \end{array} \right]

透视变换常用于图像的校正

灰度插值

  1. 最近邻插值

对于通过反向变换得到的的一个浮点坐标，对其进行简单的取整，得到一个整数型坐标，这个整数型坐标对应的像素值就是目的像素的像素值

最近邻插值的计算量较小，但可能会造成图像的灰度不连续，在灰度有变化的地方可能会出现明显的锯齿状

  1. 双线性插值

对于一个目的像素， 假设其坐标通过反向变换后得到的浮点坐标为(i+u,j+v)(i + u,j + v)，其中uu，vv为[0,1)[0,1)区间内的浮点数，则点f(i+u,j+v)f(i + u,j + v)的像素值可以由下列式子决定

f(i+u,j+v)=(1−u)(1−v)f(i,j)+(1−u)vf(i,j+1)+u(1−v)f(i+1,j)+uvf(i+1,j+1)f(i + u,j + v) = (1-u)(1-v)f(i,j) + (1-u)vf(i,j+1)+u(1-v)f(i+1,j)+uvf(i+1,j+1)

缩放后图像质量高，不会出现像素值不连续的的情况

但是由于双线性插值具有低通滤波器的性质，使得高频分量受损，所以可能会使图像轮廓在一定程度上变得模糊

  1. 双三次插值

双三次插值可以克服以上两种算法的不足，但是计算量也是最大的

此处不做赘述

图像的代数变换

就是指图像之间的加减乘除

图像的加减此处不赘述，图像的乘除主要应用于阴影校正和感兴趣区域（ROI）操作

图像的离散傅里叶变换

1D-DFT

主要用于检测含噪信号的有效成分

2D-DFT

用于得到幅度谱和相位谱

幅度谱决定了一幅图像中含有的各种频率分量的多少

相位谱决定了每一种频率分量在图像中的位置

图像的离散余弦变换

由于DFT是复数运算，其时间开销较大，不便于实时处理

若能通过函数构造等手段使得参与变换的函数为实偶函数，则最终的输出频谱序列中就仅含有实部项（余弦项）

可以用于图像压缩

形态学处理

二值数学形态学

二值形态学的运算对象为集合

然而在实际的运算过程中，当涉及到两个集合时，我们并不视其为对等的

通常设其中的一个为图像集合（用A表示） ，另一个为结构元素（用B表示）

下图表示了常用结构元的形状

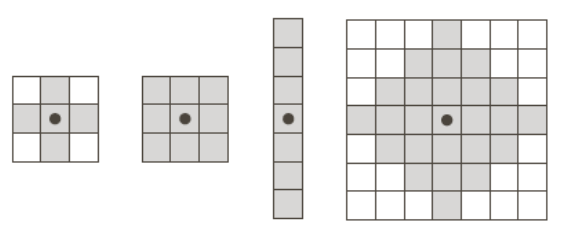
当结构元（Structuring Element， SE）对称且未指定原点位置时，则假定原点位于其对称中心处

集合论基础知识

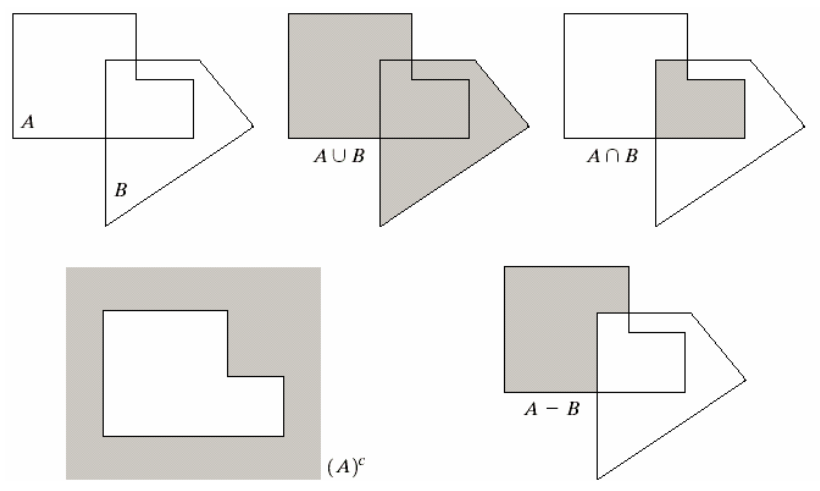
上图表示了集合之间的几个基本运算：并、交、补、差

集合BB的反射表示为B^\hat B，定义如下：

B^={w∣w=−b,b∈B}\hat B = \{w|w = -b,b\in B\}

集合BB平移到点z=(z1,z2)z = (z_1,z_2)，表示为(B)z(B)_z，其定义如下：

(B)z={c∣c=b+z,b∈B}(B)_z = \{c|c = b + z,b\in B\}

膨胀

设AA和BB是两个集合，则AA被BB膨胀可以定义为：

A⊕B={z∣(B^)z∩A≠∅}A\oplus B = \{z|(\hat B)_z\cap A\neq \varnothing \}

一般应用于桥接图像中的裂缝

腐蚀

设AA和BB是两个集合，则AA被BB腐蚀可以定义为：

AΘB={z∣(B)z⊆A}A\Theta B = \{z|(B)_z\subseteq A\}

一般应用于去除图像中的某些部分

用向量运算或者位移运算来实现膨胀和腐蚀

向量运算

将AA和BB均视为向量，则膨胀和腐蚀可分别表示为：

A⊕B={x∣x=a+b,对某些a∈A和b∈B}A\oplus B = \{x|x = a+b,对某些a\in A和b\in B\}

AΘB={x∣(x+b)∈A,对每一个b∈B}A\Theta B = \{x|(x+b)\in A,对每一个b\in B\}

位移运算

膨胀的位移运算公式如下：

A⊕B=⋃b∈B(A)bA\oplus B = \bigcup_{b\in B}(A)_b

上式表明，A⊕BA\oplus B是将AA中的每一项按每一个b∈Bb\in B移位的结果，也可以解释成：用BB来膨胀AA就是按每个bb来位移AA并把结果或（OR）起来

腐蚀的位移运算公式如下：

AΘB=⋂b∈B(A)−bA\Theta B = \bigcap_{b\in B}(A)_{-b}

上式表明，AΘBA\Theta B是将AA以所有的b∈Bb\in B进行负移位得到的交集，也可以解释成：用BB来腐蚀AA就是按每个bb来负位移AA并把结果与（AND）起来

膨胀和腐蚀的对偶性

膨胀和腐蚀这两种运算是紧密联系在一起的，一个运算对图像目标的操作相当于另一个运算对图像背景的操作，即：

(A⊕B)c=AcΘB(A\oplus B)^c = A^c\Theta B

(AΘB)c=Ac⊕B(A\Theta B)^c = A^c\oplus B

开操作和闭操作

膨胀和腐蚀并非互为逆运算，因此，可将它们结联起来使用

例如，可先执行膨胀运算，然后再基于膨胀后的结果进行腐蚀运算，或者反其道而行之，前一种运算称为闭合，后一种运算称为开启，二者也是形态学家族中的重要运算类型

开操作一般会平滑物体的轮廓、断开较窄的狭颈并消除细的突出物

闭操作同样也会平滑掉轮廓的一部分，但与开操作相反，它通常会弥合较窄的间断和细长的沟壑，消除小的孔洞，填补轮廓线中的断裂等

开操作的定义为：

A∘B=(AΘB)⊕BA\circ B = (A\Theta B)\oplus B

闭操作的定义为：

A∙B=(A⊕B)ΘBA\bullet B = (A\oplus B)\Theta B

击中-击不中变换

击中-击不中变换是形状检测的一个基本工具

一般用于在图中找出指定图形的位置

基本的二值形态学算法

边界提取

β(A)=A−(AΘB)\beta(A) = A - (A\Theta B)

因为腐蚀操作会腐蚀掉原图形边界上的一些微小的突出，将其与原图像作差则可以大致得出原图形的边界

孔洞填充

Xk=(Xk−1⊕B)∩Ac,k=1,2,3,⋯X_k = (X_{k - 1}\oplus B)\cap A^c,k = 1,2,3,\cdots

当Xk=Xk−1X_k = X_{k - 1}时，迭代停止，此时XkX_k和AA的并集就是最终的填充结果，它包括了填充了的区域内部及其边界

如果上述迭代公式的膨胀过程如果不加以控制的话，最终的结果就会超出边界，进而填充满整个区域

为了避免这种现象发生，我们在每一步之中都让膨胀的结果和AcA^c求交集，以便于让迭代膨胀的结果限制在我们感兴趣的区域之内，这种膨胀过程可以称之为条件膨胀过程

联通分量的提取

设YY代表集合AA中的一个连通分量，并假设已知YY中的一个点，那么可用
下列迭代公式得到YY的所有元素：

Xk=(Xk−1⊕B)∩A,k=1,2,3,⋯X_k = (X_{k - 1}\oplus B)\cap A,k = 1,2,3,\cdots

当Xk=Xk−1X_k = X_{k - 1}时，迭代停止，此时的结果为YY所代表的联通分量

凸壳

如果在集合AA内连接任意两个点的直线段都在AA的内部，则称集合AA是凸形的

任意集合SS的凸壳HH是包含SS的最小凸集

集合之差H−SH-S称为SS的凸缺

细化

在有些应用中，希望能腐蚀目标区域但不要将其分裂成多个子区域

这里需要先检测处在目标区域边缘处的系列像素，如果将它们除去并不会将区域分裂成多个子区域

这个工作可通过细化操作来完成

粗化

粗化从形态学角度来说是与细化对称的

在实际应用中，可以先细化背景然后再求补以得到最终的粗化结果

粗化所用的结构元可以与细化的类似，只需要将其中的1和0对换位置即可

灰度级数学形态学

灰度级数学形态学相比二值形态学，不仅要考虑像素的空间位置，还要考虑像素灰度的大小

而且灰度级形态学中的结构元包括两种类别：非平坦的和平坦的结构元

膨胀与腐蚀

未完待续…\ldots