谨以此文,献给年少轻狂的自己
为什么需要小波变换
我们目前工程实践中所分析的信号大多是平稳信号,若忽略高斯噪声,则基本可以看作严格平稳信号的信号。但是我们难免会遇到需要进行时频分析的信号,这时候就需要采用一些时频分析方法
对于非平稳信号,传统的傅里叶变换是没有办法进行很好的分析的,需要采用特殊的方法,比如短时傅里叶变换(STFT)
短时傅里叶变换是通过添加一个固定的采样窗口来进行采样,再进行FFT,最后将结果整合为时频分析结果
下面有个例子
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
clc,clf,clear;
NPT = 4000;
f1 = 100;
f2 = 150;
f3 = 200;
f4 = 300;
sample_rate = 1000;
t = 0:1 / sample_rate:(NPT - 1) / sample_rate;
raw_signal = zeros(1,NPT);
for i = 1:1000
raw_signal(i) = sin(2 * pi * f1 * t(i));
end
for i = 1001:2000
raw_signal(i) = sin(2 * pi * f2 * t(i));
end
for i = 2001:3000
raw_signal(i) = sin(2 * pi * f3 * t(i));
end
for i = 3001:4000
raw_signal(i) = sin(2 * pi * f4 * t(i));
end
raw_signal = raw_signal + rand(1,4000);
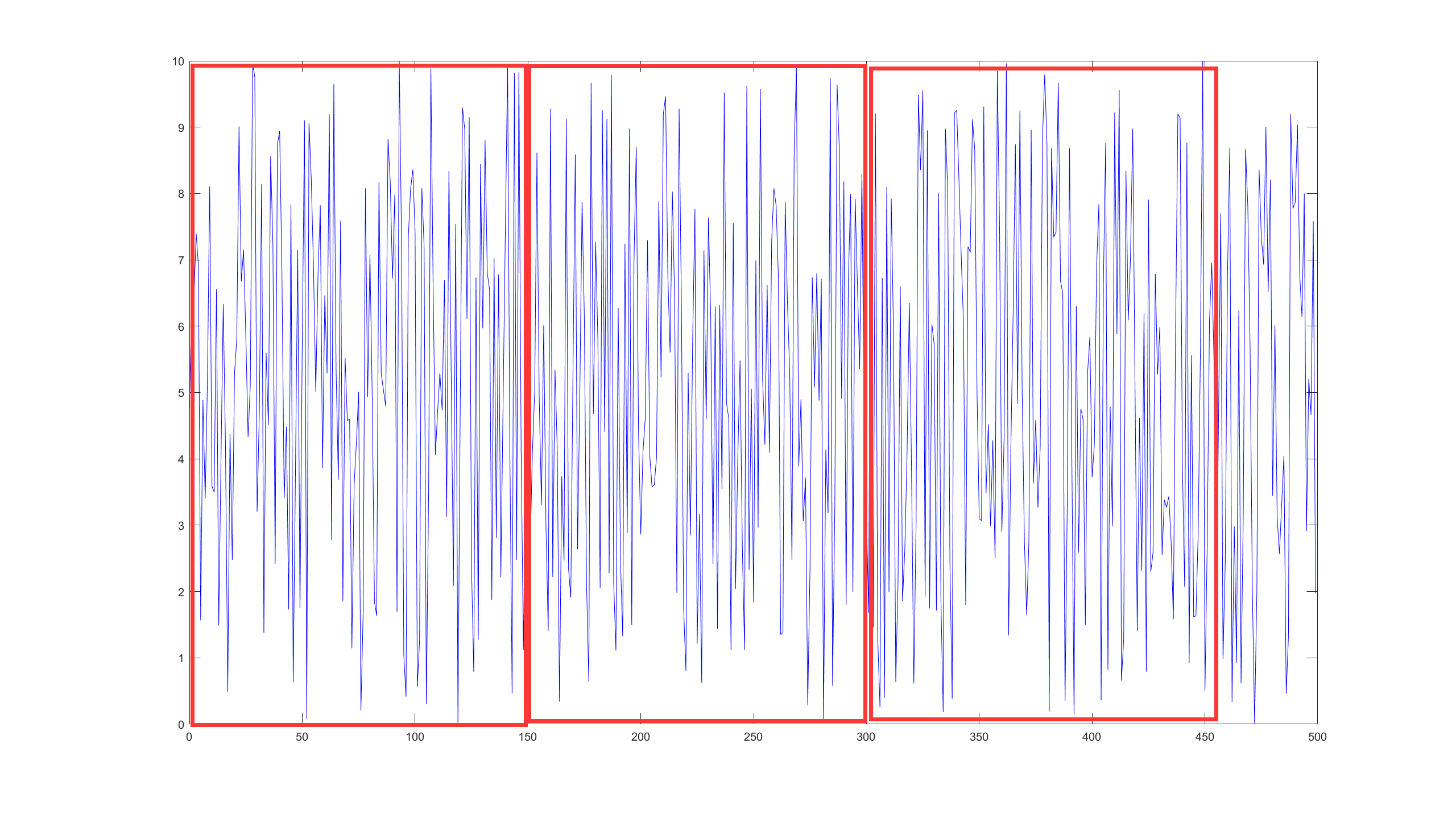
figure('Name',"波形预览");
plot(t,raw_signal,'b');
|
这是一个频率和时间有关的,且混杂了高斯噪声的正弦信号的时域图
下面我们对这个信号的整个时域采样结果进行STFT分析
1
2
3
4
5
6
7
|
result_stft = stft(raw_signal);
f_stft = -sample_rate / 2:sample_rate / (length(result_stft(:,1)) - 1):sample_rate / 2;
figure('Name',"STFT分析");
waterfall(0:length(result_stft(1,:)) - 1,f_stft,abs(result_stft).^2);
colorbar;
title("STFT分析"),xlabel("时间"),ylabel("频率/Hz");
|
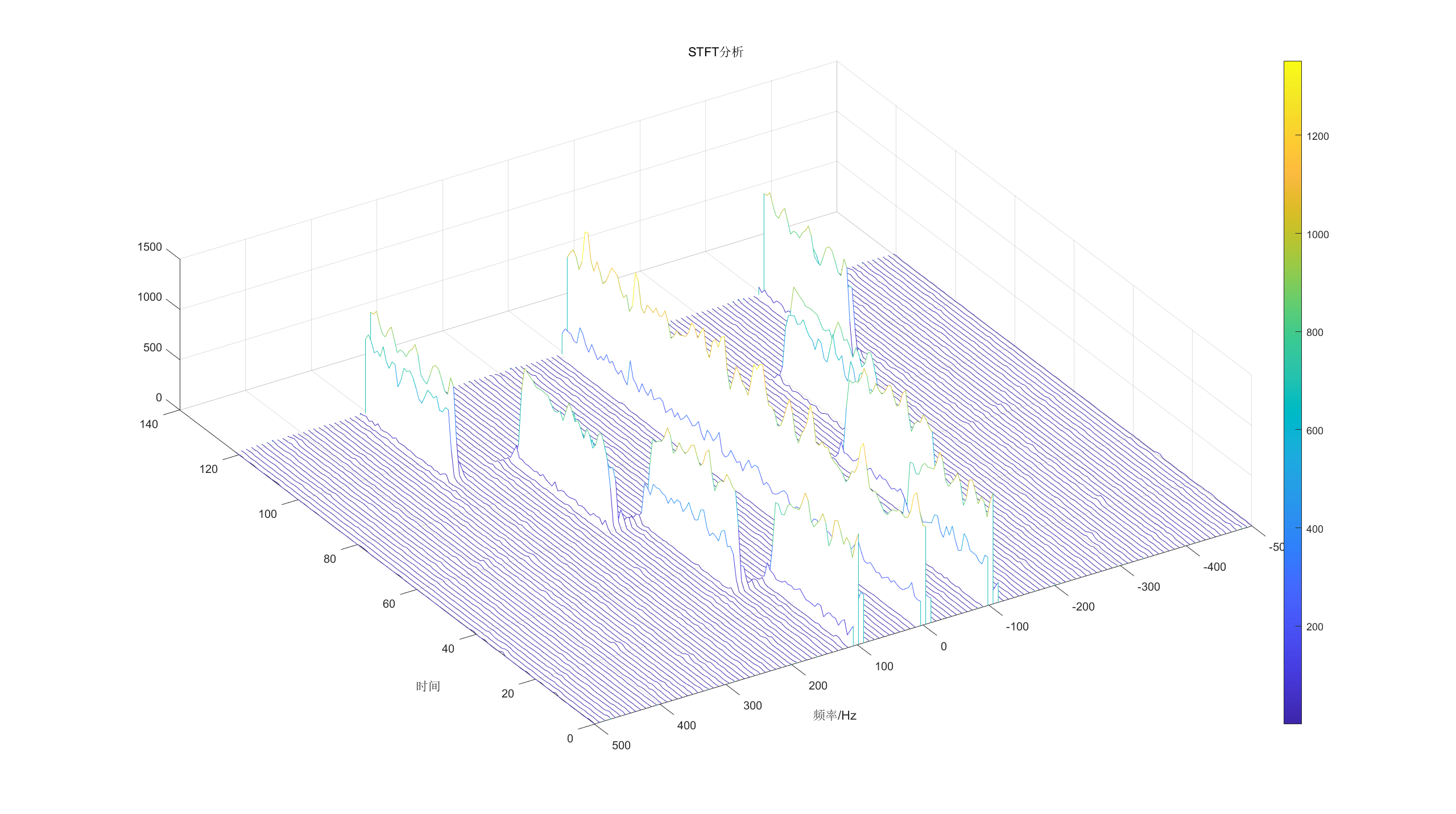
从瀑布图当中可以非常明显的看出来时频关系
下面我们再对所有的采样结果进行FFT分析
1
2
3
4
5
6
|
result_fft = fft(raw_signal);
f_fft = -sample_rate / 2:sample_rate / (length(result_fft) - 1):sample_rate / 2;
figure('Name',"FFT分析(全局)");
plot(f_fft,abs(fftshift(result_fft)),'b');
title("FFT分析(全局)"),xlabel("频率"),ylabel("幅值");
|
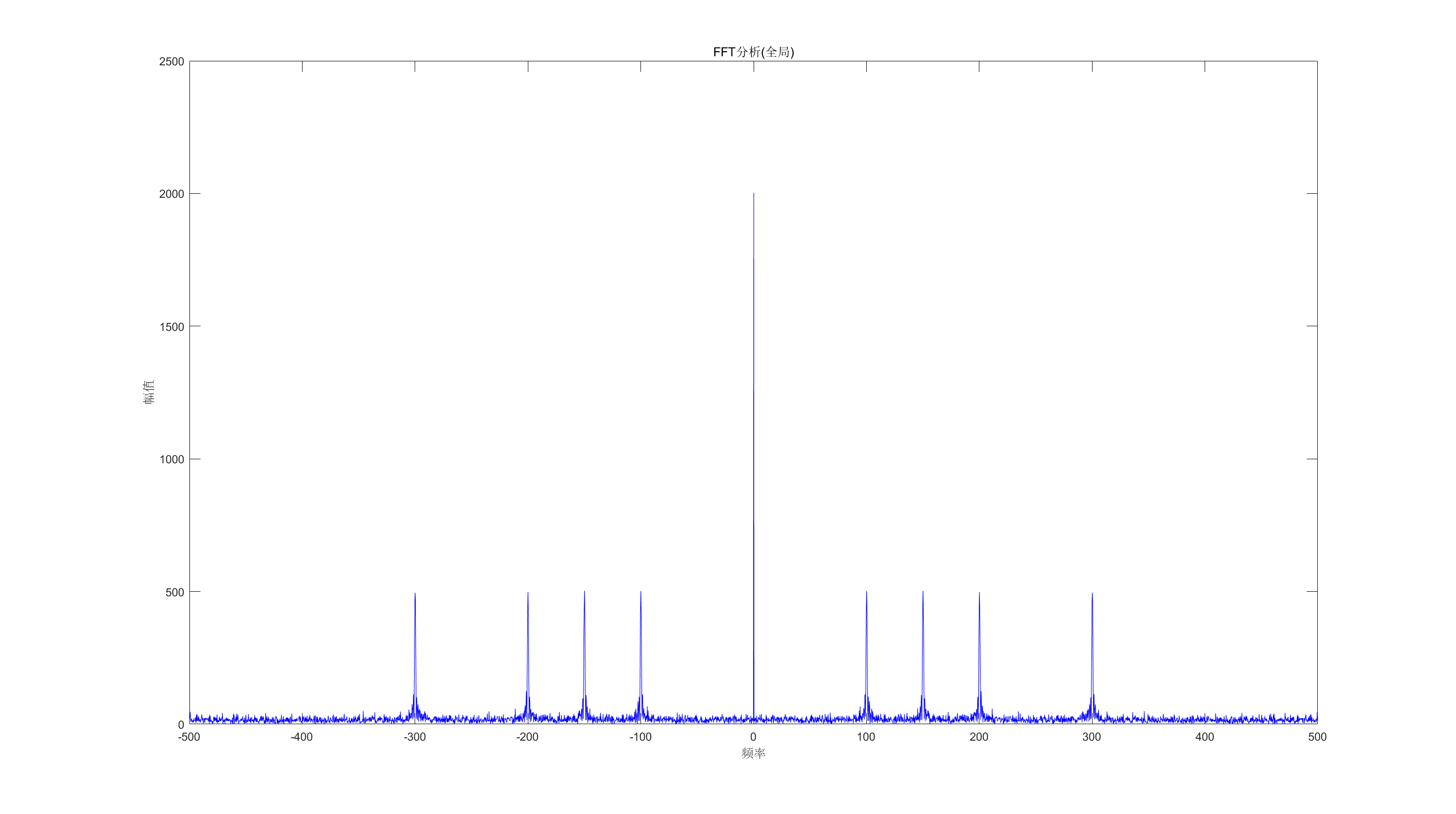
可以看到FFT确实也能得到频率信息,但是会丢失时间信息
但是我们知道,在实际工程当中,肯定是不能做到这种完全采集再分析的,所以更可能的情况是对任意一小段信号进行FFT
下面是随机抽取的一小段信号的FFT分析
1
2
3
4
5
6
|
result_fft_ano = fft(raw_signal(1000:1350));
figure('Name',"FFT分析(局部)");
f_fft_ano = -sample_rate / 2:sample_rate / (length(result_fft_ano) - 1):sample_rate / 2;
plot(f_fft_ano,abs(fftshift(result_fft_ano)),'b');
title("FFT分析(局部)"),xlabel("频率"),ylabel("幅值");
|
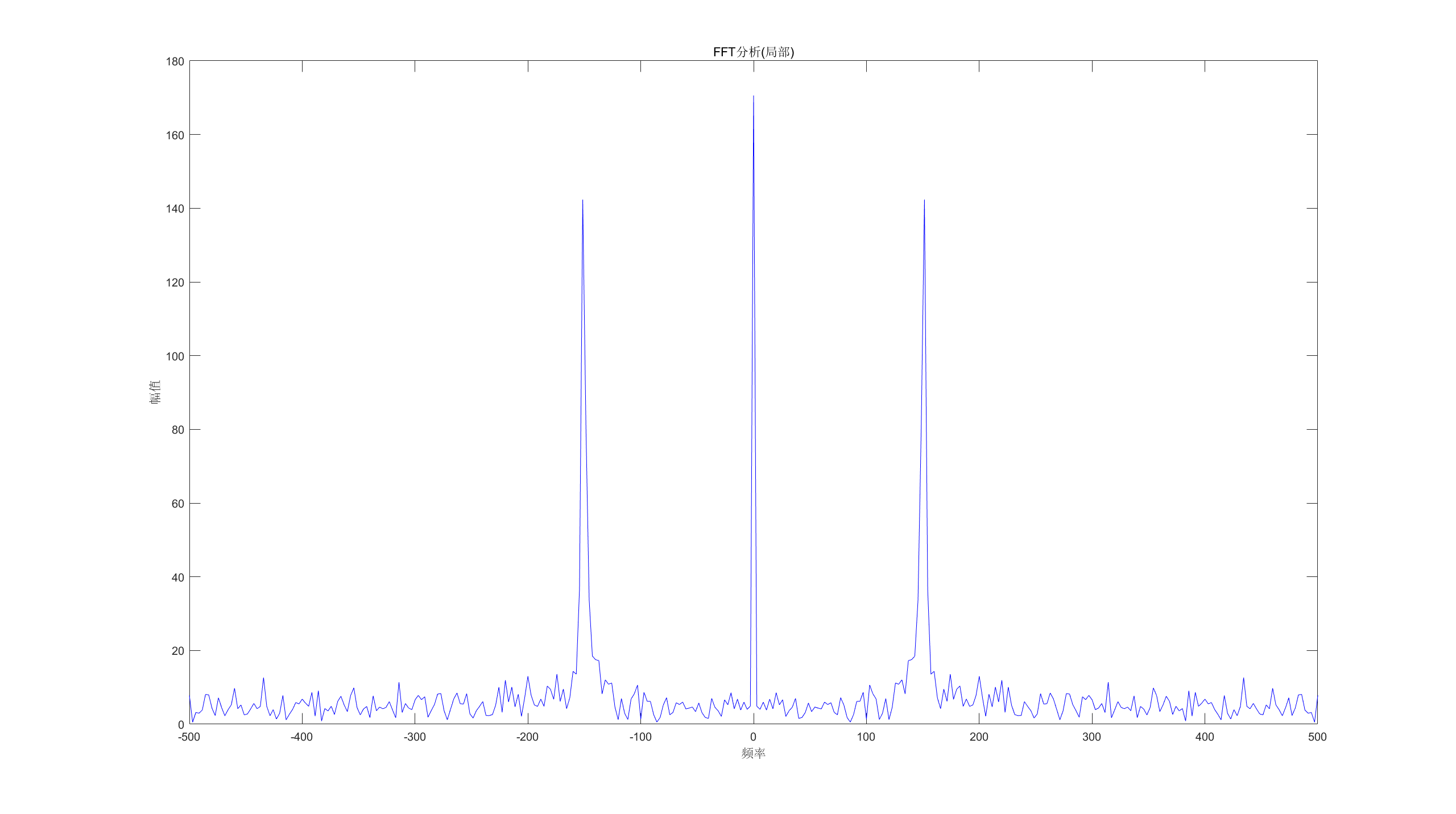
可以看到,这次不仅丢失了时间信息,还丢失了频率信息,而这就充分的说明了时频分析方法的重要性
但是对于短时傅里叶变换而言,有一个致命的缺陷,就是窗宽不好确定
这里涉及到的就是不确定原理
即,假设f为L2(R)空间的函数,它在−∞和+∞处为0,则对于任意的a∈R和α∈R,有:
Δaf⋅Δαf≥41
意思就是f在a处的分辨和f在α处的分辨不可能同时任意地小
具体证明可见《小波与傅里叶分析基础》
因为如果采样窗的长度变长了,那么时间轴的分辨率必定会下降;而采样窗的长度变短的情况下,若采样率不变,则采样点数会减少,意味着频率分辨率会下降
而且STFT的采样窗的长度是固定的,不能做到灵活可调
总的来说,缺点有二:
- 时间和频率分辨率都固定,不能随着频率的高低实现动态可调
- 选择一个合适的窗宽十分困难
而小波变换可以自由的更改时间和频率的分辨率,做到灵活可控
小波变换介绍
概念介绍
在小波分析当中,有两个函数非常重要,即尺度函数ϕ和小波函数ψ
这两个函数产生了一组可以用于分解和重构信号的函数族
在构造函数族的时候,ϕ有时候称为父小波,ψ称为母小波
需要说明,小波母函数并不是一个特定的函数,而是一种函数的集合,满足了一定条件的函数均可以作为小波母函数
小波母函数需要满足的有以下几个条件:
- 紧支撑性
用数学语言表示就是∃a∈>0,∀∣t∣>a,ψ(t)=0,即仅在很小的一部分定义域当中不为0,其他部分均为0
紧支撑性带来的好处是具有紧支撑性的基函数,在原信号的时间轴上平移,就相当于对于原信号就行了加窗操作
- 波动性
即∫−∞+∞ψ(t)dt=0,也就是说,在所有定义域内积分为0
- 容许条件
cψ=2π∫−∞∞∣f∣∣ψ(f)∣2df=0
其中,ψ(f)是小波函数傅里叶变换的共轭,这个条件使得变换可逆
- 正交性
这个条件也是为了变换可逆
过程分析
小波母函数的变换公式如下
ψ∗(τ,s)=s1ψ(st−τ)
这体现出了小波变换的两种变换方式:平移和缩放
平移是通过τ控制的,缩放是通过s控制的
再平移之后,就需要和信号相乘了,这可以筛选出在小波母函数非零部分,频率和小波母函数相近的成分
将上述过程写成公式就是
CWTxψ(τ,s)=s1∫−∞∞x(t)ψ(st−τ)dt
事实上,τ和s可以为任意数,即有无限种组合
仿真对比
1
2
3
4
5
6
7
|
cwt_result = cwt(raw_signal);
f_cwt = -sample_rate / 2:sample_rate / (length(cwt_result(:,1)) - 1):sample_rate / 2;
figure('Name',"CWT分析");
waterfall(0:length(cwt_result(1,:)) - 1,f_cwt,abs(cwt_result).^2);
colorbar;
title("CWT分析");
|
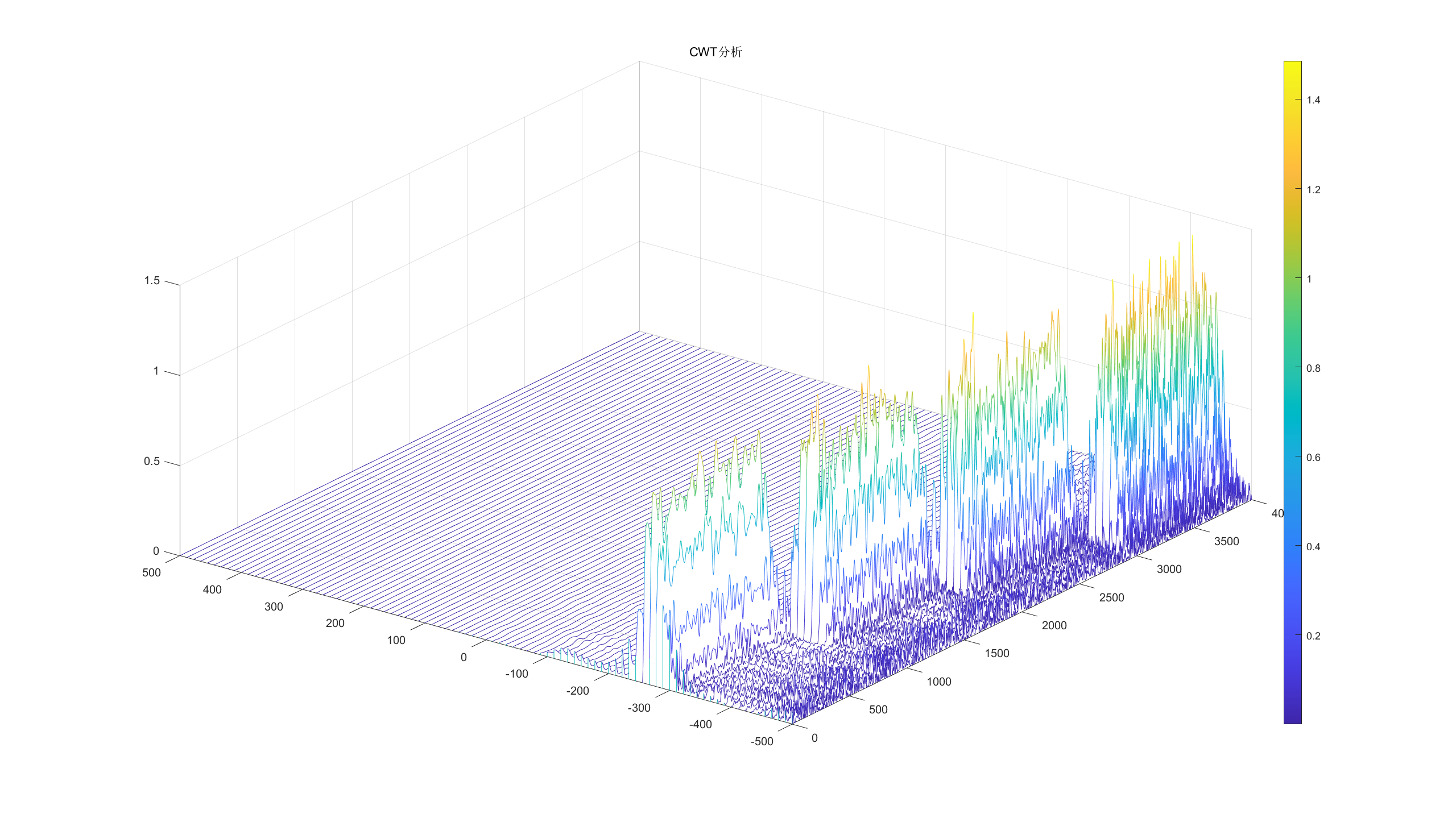
可以看到CWT的分辨率是优于STFT的
常用小波基介绍
我们常用的小波基函数就以下几种
| 小波基函数名称 |
优点 |
缺点 |
| Haar |
简单 |
性能一般 |
| Daubechies(dbN) |
常用于滤波器 |
性能和迭代次数有关 |
| Mexican Hat(mexh) |
在时间域与频率域都有很好的局部化 |
未知 |
| Morlet |
未知 |
未知 |
| Meyer |
未知 |
未知 |
下面会解释简单的Haar小波基
Haar
概念
Haar的尺度函数为
ϕ(x)=⎩⎨⎧1,0,for 0≤x<1otherwise
小波函数为
ψ(x)=⎩⎨⎧1,−1,0,for 0≤x<21for 21≤x<1otherwise
令V0是所有形如
k∈Z∑akϕ(x−k),ak∈R
的函数组成的空间,k可以在任一有限的整数范围内取值
因为ϕ(x−k)在x=k和x=k+1处不连续,换句话说,V0是所有不连续点仅在整数集中的分段常量函数所组成的空间
当然,V0的函数也可能在整数点处连续,如a1=a2的情况,和式在x=2处连续
设j是非负整数,j级阶梯空间表示为Vj,它是由函数集
{⋯,ϕ(2jx+1),ϕ(2jx),ϕ(2jx−1),ϕ(2jx−2),⋯}
在实数域上张成的,Vj是紧支撑的分段常量函数空间,其间断点在下列集合中:
{⋯,−2j1,0,2j1,2j2,2j3,⋯}
V0中的函数是在整数集上有间断点的分段常量函数,V0中任何一个函数亦属于V1,依此类推,有:
V0⊂V1⊂V2⊂V3⊂⋯Vj−1⊂Vj⊂Vj+1⊂⋯
这种包含关系是严格的,Vj包含所有在分辨率为2−j下的相关信息,随着j的增加,分辨的更精细
而Vj⊂Vj+1意味着随分辨率的提高,不会损失任何信息,该包含关系也说明了为什么Vj是以ϕ(2jx)形式而不是以ϕ(ax)形式定义的
下面不经过证明给出一个定理
函数集{22jϕ(2jx−k);k∈Z}是Vj的一个标准正交基
但是我们有了Vj的正交基之后,也只是完成了一半的任务
为了解决噪声滤除问题,我们需要一个孤立属于Vj但是不属于Vj−1的方法,于是引出了小波函数ψ
该方法就是将Vj分解成Vj−1及其正交补
令Wj是由下列函数构成的空间
k∈Z∑akψ(2jx−k)ak∈R
这里假定只有有限个ak非零,Wj是Vj的正交补,即
Vj+1=Vj⊕Wj
也就是说Vj可以不断分解下去,直到0,最后得到以下结果
Vj中的任一f可唯一地分解为以下的和式
f=wj−1+wj−2+⋯+w0+f0
其中wl∈Wl,0≤l≤j−1且f0∈V0
直观的说,wl表示宽为2l+11的”尖峰“,且不能由其他宽度的尖峰的线性组合表示
我们再次不加证明地给出以下定理
L2(R)能被分解为无限个正交直和:L2(R)=V0⊕W0⊕W1⊕⋯特别地,对于每个f∈L2(R)可以唯一的写成:f=f0+j=0∑∞wj此处f0∈V0,wj∈Wj无限直和可以视为有限直和的极限,即f=f0+N→∞limwj这里的极限是指L2意义上的极限
分解
至此,从理论上讲,噪声的滤除问题已经解决了
fj可以分解为:
fj=f0+w1+w2+⋯+wj−1,w1∈W1
其中wl表示宽为2l+11的尖峰,当l足够大时,这样的尖峰就能够表示噪声了
下面我们来实现分解算法
先用以下的阶梯函数近似原信号f:
fj(x)=i∈Z∑aiϕ(2jx−l)
该过程就是在对信号采样,采样点为x=⋯,−2j1,0,2j1,⋯从而得到al=f(2ll),l∈Z
下面不加证明地给出ϕ和ψ之间的关系式
ϕ(2jx)=(ψ(2j−1x)+ϕ(2j−1x))/2ϕ(2jx−1)=(2j−1ϕ(x)−2j−1ψ(x))/2
可以由这个关系式将原信号进行分解,最后得到以下分解公式
设fj(x)=k∈Z∑akjϕ(2jx−k)∈Vj那么fj可以分解为:fj=wj−1+fj−1这里,wj−1=k∈Z∑bkj−1ψ(2j−1x−k)∈Wj−1fj−1=k∈Z∑akj−1ψ(2j−1x−k)∈Vj−1其中,bkj−1=2a2kj−a2k+1jakj−1=2a2kj+a2k+1j该分解过程可以用j−1取代j,继续分解下去,最后得到fj=wj−1+wj−2+⋯+w0+f0
重构
至此,我们已经完成信号的分解
而我们最终的目的是信号滤波,所以下一步应该将信号重构回去
但是在此之前,我们需要丢弃一部分被视为噪声的Wj
如果是为了压缩数据,则较小幅值的Wj可以被丢弃,仅传输显著的分量,从而获得较大的压缩比
重构算法的证明可以见《小波与傅里叶分析基础》
下面我们不加证明地给出Haar重构公式
设f=f0+w0+w1+⋯+wj−1这里,f0(x)=k∈Z∑ak0ϕ(x−k)∈V0wj′(x)=k∈Z∑bkj′ψ(2j′x−k∈Wj′)其中0≤j′<j,那么f(x)−l∈Z∑aijϕ(2jx−l)∈Vj这里的alj′是根据如下算法,由j′=1,j′=2,⋯循环确定的,alj′−⎩⎨⎧akj′−1+bkj′−1,akj′−1−bkj′−1,若l=2k是偶数若l=2k+1是奇数
多分辨率分析
暂略
道阻且长,To be continued⋯







