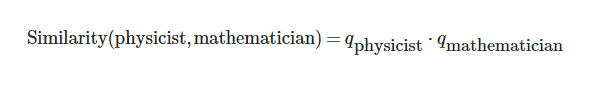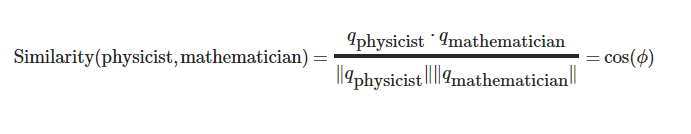NLP入门

词嵌入：编码形式的词汇语义

词嵌入是一种由真实数字组成的稠密向量，每个向量都代表了单词表里的一个单词

在自然语言处理中，总会遇到这样的情况：特征全是单词！ 但是，如何在电脑上表述一个单词呢？

你在电脑上存储的单词的 ASCII 码，但是它仅仅代表单词怎么拼写，没有说明单词的内在含义(你也许能够从词缀中了解它的词性，或者从大小写中得到一些属性，但仅此而已)

更重要的是，你能把这些 ASCII 码字符组合成什么含义？当$V$代表词汇表、输入数据是$|V|$维的情况下，我们往往想从神经网络中得到数据密集的结果，但是结果只有很少的几个维度（例如，预测的数据只有几个标签时），我们如何从大的数据维度空间中得到稍小一点的维度空间？

放弃使用 ASCII 码字符的形式表示单词，换用one-hot encoding会怎么样了？好吧，$\omega$这个单词就能这样表示：

$$\hat{y_i}\in T$$

其中，1表示的独有位置，其他位置全是0。其他的词都类似，在另外不一样的位置有一个1代表它，其他位置也都是0。这种表达除了占用巨大 的空间外，还有个很大的缺陷。它只是简单的把词看做一个单独个体，认为它们之间毫无联系。我们真正想要的是能够表达单词之间一些相似 的含义。为什么要这样做呢？来看下面的例子：

假如我们正在搭建一个语言模型，训练数据有下面一些句子：

• The mathematician ran to the store.

• The physicist ran to the store.

• The mathematician solved the open problem.

现在又得到一个没见过的新句子：

• The physicist solved the open problem.

我们的模型可能在这个句子上表现的还不错，但是，如果利用了下面两个事实，模型会表现更佳：

• 我们发现数学家和物理学家在句子里有相同的作用，所以在某种程度上，他们有语义的联系。

• 当看见物理学家在新句子中的作用时，我们发现数学家也有起着相同的作用。

然后我们就推测，物理学家在上面的句子里也类似于数学家吗？这就是我们所指的相似性理念： 指的是语义相似，而不是简单的拼写相似。 这就是一种通过连接我们发现的和没发现的一些内容相似点、用于解决语言数据稀疏性的技术。这个例子依赖于一个基本的语言假设：那些在 相似语句中出现的单词，在语义上也是相互关联的。这就叫做distributional hypothesis（分布式假设）

Getting Dense Word Embeddings（密集词嵌入）

我们如何解决这个问题呢？也就是，怎么编码单词中的语义相似性？ 也许我们会想到一些语义属性。 举个例子，我们发现数学家和物理学家都能跑，所以也许可以给含有“能跑”语义属性的单词打高分，考虑一下其他的属性，想象一下你可能会在这些属性上给普通的单词打什么分

如果每个属性都表示一个维度，那我们也许可以用一个向量表示一个单词，就像这样：

那么，我们就这可以通过下面的方法得到这些单词之间的相似性：

尽管通常情况下需要进行长度归一化：

其中$\phi$是两个向量的夹角

这就意味着，完全相似的单词相似度为1。完全不相似的单词相似度为-1

你可以把本章开头介绍的one-hot稀疏向量看做是我们新定义向量的一种特殊形式，那里的单词相似度为0，现在我们给每个单词一些独特的语义属性，这些向量数据密集，也就是说它们数字通常都非零

但是新的这些向量存在一个严重的问题：你可以想到数千种不同的语义属性，它们可能都与决定相似性有关，而且，到底如何设置不同属性的值呢？

深度学习的中心思想是用神经网络来学习特征的表示，而不是程序员去设计它们，所以为什么不把词嵌入只当做模型参数，而是通过训 练来更新呢？

这就才是我们要确切做的事。我们将用神经网络做一些潜在语义属性，但是原则上，学习才是关键

注意，词嵌入可能无法解释

也就是说，尽管使用我们上面手动制作的向量，能够发现数学家和物理学家都喜欢喝咖啡的相似性，如果我们允许神经网络来学习词嵌入，那么就会发现数学家和物理学家在第二维度有个较大的值，它所代表的含义很不清晰

它们在一些潜在语义上是相似的，但是对我们来说无法解释

Pytorch中的词嵌入

在我们举例或练习之前，这里有一份关于如何在Pytorch和常见的深度学习中使用词嵌入的简要介绍

与制作one-hot向量时对每个单词定义一个特殊的索引类似，当我们使用词向量时也需要为每个单词定义一个索引，这些索引将是查询表的关键点

意思就是，词嵌入被被存储在一个$|V|\times D$的向量中，其中$D$是词嵌入的维度。词被分配的索引$i$，表示在向量的第$i$行存储它的嵌入

在所有的代码中，从单词到索引的映射是一个叫word_to_ix的字典

能使用词嵌入的模块是torch.nn.Embedding，这里面有两个参数：词汇表的大小和词嵌入的维度

索引这张表时，你必须使用torch.LongTensor（因为索引是整数，不是浮点数）

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

word_to_ix = {"hello": 0, "world": 1}
embeds = nn.Embedding(2, 5)  # 2 words in vocab, 5 dimensional embeddings
lookup_tensor = torch.tensor([word_to_ix["hello"]], dtype=torch.long)
hello_embed = embeds(lookup_tensor)
print(hello_embed)

例子： N-Gram语言模型

回想一下，在n-gram语言模型中，给定一个单词序列向量，我们要计算的是：

$$P(\omega_i|\omega_{i-1},\omega_{i-2},\ldots,\omega_{i-n+1})$$

其中$\omega_i$是单词序列的第$i$个单词

在本例中，我们将在训练样例上计算损失函数，并且用反向传播算法更新参数

CONTEXT_SIZE = 2
EMBEDDING_DIM = 10
# 我们用莎士比亚的十四行诗 Sonnet 2
test_sentence = """When forty winters shall besiege thy brow,
And dig deep trenches in thy beauty's field,
Thy youth's proud livery so gazed on now,
Will be a totter'd weed of small worth held:
Then being asked, where all thy beauty lies,
Where all the treasure of thy lusty days;
To say, within thine own deep sunken eyes,
Were an all-eating shame, and thriftless praise.
How much more praise deserv'd thy beauty's use,
If thou couldst answer 'This fair child of mine
Shall sum my count, and make my old excuse,'
Proving his beauty by succession thine!
This were to be new made when thou art old,
And see thy blood warm when thou feel'st it cold.""".split()
# 应该对输入变量进行标记，但暂时忽略。
# 创建一系列的元组，每个元组都是([ word_i-2, word_i-1 ], target word)的形式。
trigrams = [([test_sentence[i], test_sentence[i + 1]], test_sentence[i + 2])
            for i in range(len(test_sentence) - 2)]
# 输出前3行，先看下是什么样子。
print(trigrams[:3])

vocab = set(test_sentence)
word_to_ix = {word: i for i, word in enumerate(vocab)}

class NGramLanguageModeler(nn.Module):

    def __init__(self, vocab_size, embedding_dim, context_size):
        super(NGramLanguageModeler, self).__init__()
        self.embeddings = nn.Embedding(vocab_size, embedding_dim)
        self.linear1 = nn.Linear(context_size * embedding_dim, 128)
        self.linear2 = nn.Linear(128, vocab_size)

    def forward(self, inputs):
        embeds = self.embeddings(inputs).view((1, -1))
        out = F.relu(self.linear1(embeds))
        out = self.linear2(out)
        log_probs = F.log_softmax(out, dim=1)
        return log_probs

losses = []
loss_function = nn.NLLLoss()
model = NGramLanguageModeler(len(vocab), EMBEDDING_DIM, CONTEXT_SIZE)
optimizer = optim.SGD(model.parameters(), lr=0.001)

for epoch in range(10):
    total_loss = 0
    for context, target in trigrams:

        # 步骤 1\. 准备好进入模型的数据 (例如将单词转换成整数索引,并将其封装在变量中)
        context_idxs = torch.tensor([word_to_ix[w] for w in context], dtype=torch.long)

        # 步骤 2\. 回调torch累乘梯度
        # 在传入一个新实例之前，需要把旧实例的梯度置零。
        model.zero_grad()

        # 步骤 3\. 继续运行代码，得到单词的log概率值。
        log_probs = model(context_idxs)

        # 步骤 4\. 计算损失函数（再次注意，Torch需要将目标单词封装在变量里）。
        loss = loss_function(log_probs, torch.tensor([word_to_ix[target]], dtype=torch.long))

        # 步骤 5\. 反向传播更新梯度
        loss.backward()
        optimizer.step()

        # 通过调tensor.item()得到单个Python数值。
        total_loss += loss.item()
    losses.append(total_loss)
print(losses)  # 用训练数据每次迭代，损失函数都会下降。

练习：计算连续词袋模型的词向量

连续词袋模型（CBOW）在NLP深度学习中使用很频繁，它是一个模型，尝试通过目标词前后几个单词的文本，来预测目标词

这有别于语言模型， 因为CBOW不是序列的，也不必是概率性的

CBOW常用于快速地训练词向量，得到的嵌入用来初始化一些复杂模型的嵌入

通常情况下，这被称为预训练嵌入，它几乎总能帮忙把模型性能提升几个百分点

CBOW 模型如下所示：给定一个单词$\omega_i$，$N$代表两边的滑窗距，如$\omega_{i-1},\omega_{i-2},\ldots,\omega_{i-N}$和$\omega_{i+1},\omega_{i+2},\ldots,\omega_{i+N}$， 并将所有的上下文词统称为$C$，CBOW试图最小化

$$-\log p(\omega_i|C) = -\log{Softmax(A(\sum_{\omega\in C}q_\omega)+b)}$$

其中$q_\omega$是单词$\omega_i$的嵌入

在Pytorch中，通过填充下面的类来实现这个模型，有两条需要注意：

• 考虑下你需要定义哪些参数

• 确保你知道每步操作后的结构，如果想重构，请使用.view()

CONTEXT_SIZE = 2  # 左右各两个词
raw_text = """We are about to study the idea of a computational process.
Computational processes are abstract beings that inhabit computers.
As they evolve, processes manipulate other abstract things called data.
The evolution of a process is directed by a pattern of rules
called a program. People create programs to direct processes. In effect,
we conjure the spirits of the computer with our spells.""".split()

# 通过对`raw_text`使用set()函数，我们进行去重操作
vocab = set(raw_text)
vocab_size = len(vocab)

word_to_ix = {word: i for i, word in enumerate(vocab)}
data = []
for i in range(2, len(raw_text) - 2):
    context = [raw_text[i - 2], raw_text[i - 1],
               raw_text[i + 1], raw_text[i + 2]]
    target = raw_text[i]
    data.append((context, target))
print(data[:5])

class CBOW(nn.Module):

    def __init__(self):
        pass

    def forward(self, inputs):
        pass

# 创建模型并且训练。这里有些函数帮你在使用模块之前制作数据。

def make_context_vector(context, word_to_ix):
    idxs = [word_to_ix[w] for w in context]
    return torch.tensor(idxs, dtype=torch.long)

make_context_vector(data[0][0], word_to_ix)  # example

序列模型和长短句记忆（LSTM）模型

• 前馈网络

之前我们已经学过了许多的前馈网络，所谓前馈网络，就是不会保存状态的网络，然而有时这并不是我们想要的效果

在自然语言处理 (NLP, Natural Language Processing) 中，序列模型是一个核心的概念

• 序列模型

所谓序列模型，即输入依赖于时间信息的模型

一个典型的序列模型是隐马尔科夫模型 (HMM, Hidden Markov Model)

另一个序列模型的例子是条件随机场 (CRF, Conditional Random Field)

• 循环神经网络

循环神经网络是指可以保存某种状态的神经网络

比如说，神经网络中上个时刻的输出可以作为下个时刻的输入的一部分，以此信息就可以通过序列在网络中一直往后传递

对于LSTM (Long-Short Term Memory) 来说，序列中的每个元素都有一个相应的隐状态，该隐状态原则上可以包含序列当前结点之前的任一节点的信息

我们可以使用隐藏状态来预测语言模型中的单词，词性标签以及其他

Pytorch中的LSTM

在正式学习之前，有几个点要说明一下：Pytorch中LSTM的输入形式是一个3D的Tensor，每一个维度都有重要的意义，第一个维度就是序列本身，第二个维度是mini-batch中实例的索引，第三个维度是输入元素的索引，我们之前没有接触过mini-batch，所以我们就先忽略它并假设第二维的维度是1

如果要用"The cow jumped"这个句子来运行一个序列模型，那么就应该把它整理成如下的形式：

除了有一个额外的大小为1的第二维度

此外, 你还可以向网络逐个输入序列, 在这种情况下, 第一个轴的大小也是1

来看一个简单的例子

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

lstm = nn.LSTM(3, 3)  # 输入维度为3维，输出维度为3维
inputs = [torch.randn(1, 3) for _ in range(5)]  # 生成一个长度为5的序列

# 初始化隐藏状态.
hidden = (torch.randn(1, 1, 3),
          torch.randn(1, 1, 3))
for i in inputs:
    # 将序列中的元素逐个输入到LSTM.
    # 经过每步操作,hidden 的值包含了隐藏状态的信息.
    out, hidden = lstm(i.view(1, 1, -1), hidden)

# 另外我们可以对一整个序列进行训练.
# LSTM第一个返回的第一个值是所有时刻的隐藏状态
# 第二个返回值是最后一个时刻的隐藏状态
#(所以"out"的最后一个和"hidden"是一样的)
# 之所以这样设计:
# 通过"out"你能取得任何一个时刻的隐藏状态，而"hidden"的值是用来进行序列的反向传播运算, 具体方式就是将它作为参数传入后面的 LSTM 网络.

# 增加额外的第二个维度.
inputs = torch.cat(inputs).view(len(inputs), 1, -1)
hidden = (torch.randn(1, 1, 3), torch.randn(1, 1, 3))  # 清空隐藏状态. 
out, hidden = lstm(inputs, hidden)
print(out)
print(hidden)

例子：用LSTM来进行词性标注

在这部分, 我们将会使用一个 LSTM 网络来进行词性标注

该模型如下：输入的句子是$\omega_1,\ldots,\omega_M$，其中$\omega_i\in V$，标签的集合定义为 $T$，$y_i$为单词$\omega_i$的标签，用$\hat{y_i}$表示对单词$\omega_i$词性的预测。

这是一个结构预测模型, 我们的输出是一个序列$\hat{y_i},\ldots,\hat{y_M}$, 其中$\hat{y_i}\in T$

在进行预测时, 需将句子每个词输入到一个LSTM网络中，将时刻$i$的隐藏状态标记为$h_i$，同样地，对每个标签赋一个独一无二的索引(类似word embeddings部分word_to_ix的设置)，然后就得到了$\hat{y_i}$的预测规则：

$$\hat{y_i} = argmax_j(\log Softmax(Ah_i + b))_j$$

即先对隐状态进行一个仿射变换，然后计算一个对数softmax，最后得到的预测标签即为对数softmax中最大的值对应的标签

注意，这也意味着$A$空间的维度是$|T|$

准备数据

def prepare_sequence(seq, to_ix):
    idxs = [to_ix[w] for w in seq]
    return torch.tensor(idxs, dtype=torch.long)

training_data = [
    ("The dog ate the apple".split(), ["DET", "NN", "V", "DET", "NN"]),
    ("Everybody read that book".split(), ["NN", "V", "DET", "NN"])
]
word_to_ix = {}
for sent, tags in training_data:
    for word in sent:
        if word not in word_to_ix:
            word_to_ix[word] = len(word_to_ix)
print(word_to_ix)
tag_to_ix = {"DET": 0, "NN": 1, "V": 2}

# 实际中通常使用更大的维度如32维, 64维.
# 这里我们使用小的维度, 为了方便查看训练过程中权重的变化.
EMBEDDING_DIM = 6
HIDDEN_DIM = 6

创建模型

class LSTMTagger(nn.Module):

    def __init__(self, embedding_dim, hidden_dim, vocab_size, tagset_size):
        super(LSTMTagger, self).__init__()
        self.hidden_dim = hidden_dim

        self.word_embeddings = nn.Embedding(vocab_size, embedding_dim)

        # LSTM以word_embeddings作为输入, 输出维度为 hidden_dim 的隐藏状态值
        self.lstm = nn.LSTM(embedding_dim, hidden_dim)

        # 线性层将隐藏状态空间映射到标注空间
        self.hidden2tag = nn.Linear(hidden_dim, tagset_size)
        self.hidden = self.init_hidden()

    def init_hidden(self):
        # 一开始并没有隐藏状态所以我们要先初始化一个
        # 关于维度为什么这么设计请参考Pytoch相关文档
        # 各个维度的含义是 (num_layers, minibatch_size, hidden_dim)
        return (torch.zeros(1, 1, self.hidden_dim),
                torch.zeros(1, 1, self.hidden_dim))

    def forward(self, sentence):
        embeds = self.word_embeddings(sentence)
        lstm_out, self.hidden = self.lstm(
            embeds.view(len(sentence), 1, -1), self.hidden)
        tag_space = self.hidden2tag(lstm_out.view(len(sentence), -1))
        tag_scores = F.log_softmax(tag_space, dim=1)
        return tag_scores

训练模型

model = LSTMTagger(EMBEDDING_DIM, HIDDEN_DIM, len(word_to_ix), len(tag_to_ix))
loss_function = nn.NLLLoss()
optimizer = optim.SGD(model.parameters(), lr=0.1)

# 查看训练前的分数
# 注意: 输出的 i,j 元素的值表示单词 i 的 j 标签的得分
# 这里我们不需要训练不需要求导，所以使用torch.no_grad()
with torch.no_grad():
    inputs = prepare_sequence(training_data[0][0], word_to_ix)
    tag_scores = model(inputs)
    print(tag_scores)

for epoch in range(300):  # 实际情况下你不会训练300个周期, 此例中我们只是随便设了一个值
    for sentence, tags in training_data:
        # 第一步: 请记住Pytorch会累加梯度.
        # 我们需要在训练每个实例前清空梯度
        model.zero_grad()

        # 此外还需要清空 LSTM 的隐状态,
        # 将其从上个实例的历史中分离出来.
        model.hidden = model.init_hidden()

        # 准备网络输入, 将其变为词索引的 Tensor 类型数据
        sentence_in = prepare_sequence(sentence, word_to_ix)
        targets = prepare_sequence(tags, tag_to_ix)

        # 第三步: 前向传播.
        tag_scores = model(sentence_in)

        # 第四步: 计算损失和梯度值, 通过调用 optimizer.step() 来更新梯度
        loss = loss_function(tag_scores, targets)
        loss.backward()
        optimizer.step()

# 查看训练后的得分
with torch.no_grad():
    inputs = prepare_sequence(training_data[0][0], word_to_ix)
    tag_scores = model(inputs)

    # 句子是 "the dog ate the apple", i,j 表示对于单词 i, 标签 j 的得分.
    # 我们采用得分最高的标签作为预测的标签. 从下面的输出我们可以看到, 预测得
    # 到的结果是0 1 2 0 1. 因为 索引是从0开始的, 因此第一个值0表示第一行的
    # 最大值, 第二个值1表示第二行的最大值, 以此类推. 所以最后的结果是 DET
    # NOUN VERB DET NOUN, 整个序列都是正确的!
    print(tag_scores)

练习：使用字符级特征来增强 LSTM 词性标注器

在上面的例子中，每个词都有一个词嵌入，作为序列模型的输入

接下来让我们使用每个的单词的字符级别的表达来增强词嵌入

我们期望这个操作对结果能有显著提升，因为像词缀这样的字符级信息对于词性有很大的影响，比如说，像包含词缀-ly的单词基本上都是被标注为副词

具体操作如下：用$c_\omega$的字符级表达, 同之前一样，我们使用$x_\omega$来表示词嵌入。序列模型的输入就变成了$c_\omega$和$x_\omega$的拼接。因此, 如果$x_\omega$的维度是5，$c_\omega$的维度是3，那么我们的LSTM网络的输入维度大小就是8

为了得到字符级别的表达, 将单词的每个字符输入一个LSTM网络, 而$c_\omega$则为这个LSTM网络最后的隐状态

一些提示：

• 新模型中需要两个LSTM, 一个跟之前一样, 用来输出词性标注的得分, 另外一个新增加的用来获取每个单词的字符级别表达

• 为了在字符级别上运行序列模型，你需要用嵌入的字符来作为字符LSTM的输入