Pytorch学习（基础知识）

参考的书籍是《深入浅出PyTorch——从模型到源码》，书中源代码仓库为https://github.com/zxjzxj9/PyTorchIntroduction

部分代码由于版本兼容性无法运行，文中会做出适当修改

前言

众所周知，炼丹现在已经成为当下最热门的方向，当然这也是因为大家看到了人工智能的前景和潜力

我在本科阶段也多次使用Pytorch进行过模型的训练，但是我总是困惑于一些代码的运作方式，有时候为了深究这些，会花费大量的时间对一些代码进行整合

除此之外，当我有一些新奇的想法时，也很难将其在Pytorch的框架下付诸实践，因为我不懂代码之间是如何配合的，类之间的关系是什么，类的方法该怎么用，我都是一知半解的三脚猫

综上，我终于下定决心，静下心来阅读Pytorch源码，为了打好基础，也是为了提高我的惨不忍睹的代码水平

由于前序课程学习了基础的机器学习的知识，所以此处直接略过理论部分的讲解，直接阅读源码

此处使用的Pytorch版本为1.13.1，Python版本为3.9.19，CUDA版本为12.5，可以用以下代码检查Pytorch版本

import torch
print(torch.__version__)

学习路径

由于篇幅限制，我决定将源码学习分为多篇文章依次进行更新，以下为推荐的博客学习路径

1. Pytorch学习（基础知识）
2. Pytorch学习（运行逻辑）
3. Pytorch高级应用

Pytorch基本操作

Pytorch包的基本结构

Pytorch有许多模块，其中主要的16个模块如下所示

torch模块

torch模块本身包含了PyTorch经常使用的一些激活函数，比如Sigmoid（torch.sigmoid）、ReLU（torch.relu）和Tanh（torch.tanh），以及 PyTorch张量的一些操作，比如矩阵的乘法（torch.mm）、张量元素的选择（torch.select）

需要注意的是，这些操作的对象大多数都是张量，因此，传入的参数需要是PyTorch的张量，否则会报错（一般报类型错误，即TypeError）

另外，还有一类函数能够产生一定形状的张量，比如torch.zeros产生元素全为0的张量，torch.randn产生元素服从标准正态分布的张量等

torch.Tensor模块

torch.Tensor模块定义了torch中的张量类型，其中的张量有不同的数值类型，如单精度、双精度浮点、整数类型等，而且张量有一定的维数和形状

同时，张量的类中也包含着一系列的方法，返回新的张量或者更改当前的张量

torch.Storage则负责torch.Tensor底层的数据存储，即为一个张量分配连续的一维内存地址（用于存储相同类型的一系列元素，数目则为张量的总元素数目）

此处简要介绍一下张量的底层存储逻辑

假如有一个$k$维的张量，它的维数为（$n_1$，$n_2$，$\cdots$，$n_k$），由于计算机的内存是连续的地址空间，所以在实际存储过程中存储的是1维的向量，这个向量在内存中的大小为$n_1\times n_2\times\cdots\times n_k$

实际数值的排列方式可以从两个方向开始（从$n_1$到$n_k$或者从$n_k$到$n_1$），一般选择从$n_k$这个维度开始，由小到大排列这个向量，即先填满$n_k$的维度，再逐渐填满$n_{k-1}$，直到$n_1$的维度

假设有1个元素，它在张量中的具体下标是（$i_1,i_2,\cdots,i_k$），那么它在内存中是第$i_1\times(n_2\times n_3\times\cdots\times n_k)+i_2\times(n_3\times\cdots\times n_k)+\cdots+i_{k-1}\times n_k+i_k$个元素，我们称每个维度位置乘以的系数，即$(n_2\times n_3\times\cdots\times n_k),(n_3\times\cdots\times n_k),\cdots,1$为这个维度的步长（Stride）或者系数（Offset）

张量在内存中的排列方式如下表所示

000	001	002	003	010	011	012	013	100	101	102	103	110	111	112	113

可以看到，维度序数较小（比如第1或第2个维度）的相邻数字在内存中的间隔比较大，反之，在内存中的间隔比较小

如果张量的某个类方法会返回张量，按照PyTorch中的命名规则，如果张量方法后缀带下画线，则该方法会修改张量本身的数据，反之则会返回新的张量

比如，Tensor.add方法会让当前张量和输入参数张量做加法，返回新的张量，而Tensor.add_方法会改变当前张量的值，新的值为旧的值和输入参数之和

torch.sparse模块

torch.sparse模块定义了稀疏张量，其中构造的稀疏张量采用的是COO存储格式（Coordinate），主要方法是用一个长整型定义非零元素的位置，用浮点数张量定义对应非零元素的值，然后利用三元组进行存储，如图所示

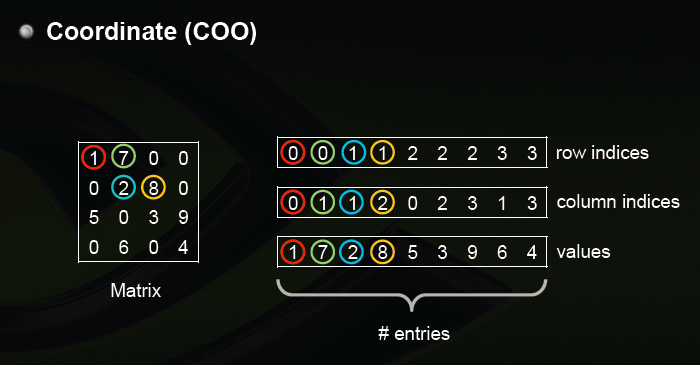
稀疏张量之间可以做元素加、减、乘、除运算和矩阵乘法

torch.cuda模块

torch.cuda模块定义了与CUDA运算相关的一系列函数，包括但不限于检查系统的CUDA是否可用，当前进程对应的GPU序号（在多GPU情况下），清除GPU上的缓存，设置GPU的计算流（Stream），同步GPU上执行的所有核函数（Kernel）等

torch.nn模块

torch.nn是Pytorch神经网络模块化的核心，其中定义了一系列模块，包括卷积层nn.ConvNd（$N = 1,2,3$）和线性层（全连接层）nn.Linear等

当构建深度学习模型的时候，可以通过调用或者继承nn.Module类并重写forward方法来实现一个新的神经网络

除此之外，torch.nn中也定义了一系列的损失函数，包括平方损失函数（torch.nn.MSELoss）、交叉熵损失函数（torch.nn.CrossEntropyLoss）等

一般而言，torch.nn里面定义的神经网络模块都含有参数，可以对这些参数使用优化器进行训练

torch.nn.functional模块

torch.nn.functional是PyTorch的函数模块，定义了一些核神经网络相关的函数，包括卷积函数和池化函数等，这些函数也是深度学习模型构建的基础

需要注意的是，torch.nn中定义的模块一般会调用torch.nn.functional里的函数，比如nn.ConvNd模块（$N = 1,2,3$）会调用torch.nn.functional.convNd函数（$N = 1,2,3$）

另外torch.nn.functional里面还定义了一些不常用的激活函数，包括torch.nn.functional.relu6和torch.nn.functional.elu等

torch.nn.init模块

torch.nn.init模块定义了神经网络权重的初始化，如果初始的神经网络权重取值不合适，就会导致后续的优化过程收敛很慢，甚至不收敛

这个模块中的函数就是为了解决神经网络权重的初始化问题，其中使用了很多初始化方法，包括均匀初始化torch.nn.init.uniform和正态分布归一化torch.nn.init.normal等

在PyTorch中函数或者方法如果以下划线结尾，则这个方法会直接改变作用张量的值，因此，这些方法会直接改变传入张量的值，同时会返回改变后的张量

torch.optim模块

torch.optim模块定义了一系列的优化器，包括但不限于torch.optim.SGD（随机梯度下降算法）、torch.optim.Adagrad（AdaGrad算法）、torch.optim.RMSprop（RMSProp算法）和torch.optim.Adam（Adam算法）等

这个模块还包含了学习率衰减的子模块，例如torch.optim.lr_scheduler，这个子模块中包含了诸如学习率阶梯下降算法torch.optim.lr_scheduler.StepLR和余弦退火算法torch.optim.lr_scheduler.CosineAnnealingLR等学习率衰减算法

torch.autograd模块

torch.autograd模块是Pytorch的自动微分算法模块，定义了一系列的自动微分函数，包括torch.autograd.backward函数，主要用于在求得损失函数之后进行反向梯度传播，torch.autograd.grad函数用于一个标量张量（即只有一个分量的张量）对另一个张量求导，以及在代码中设置不参与求导的部分

另外，这个模块还内置了数值梯度功能和检查自动微分引擎是否输出正确结果的功能

torch.distributed模块

torch.distributed是PyTorch的分布式计算模块，主要功能是提供PyTorch并行运行环境，其主要支持的后端有MPI、GIoo和NCCL三种

PyTorch的分布式工作原理主要是启动多个并行的进程，每个进程都拥有一个模型的备份，然后输入不同的训练数据到多个并行的进程，计算损失函数，每个进程独立地做反向传播，最后对所有进程权重张量的梯度做归约（Reduce）

用到后端的部分主要是数据的广播（Broadcast）和数据的收集（Gather），其中，前者是把数据从一个节点（进程）传播到另一个节点（进程），比如归约后梯度张量的传播，后者则是把数据从其他节点（进程）转移到当前节点（进程），比如把梯度张量从其他节点转移到某个特定的节点，然后对所有的张量求平均

PyTorch的分布式计算模块不但提供了后端的一个包装，还提供了一些启动方式来启动多个进程，包括但不于通过网络（TCP）、通过环境变量、通过共享文件等

torch.distributions模块

torch.distributions模块提供了一系列类，使得PyTorch能够对不同的分布进行采
样，并且生成概率采样过程的计算图

在一些应用过程中，比如强化学习（Reinforcement Learning），经常会使用一个深度学习模型来模拟在不同环境条件下采取的策略（Policy），其最后的输出是不同动作的概率

当深度学习模型输出概率之后，需要根据概率对策略进行采样来模拟当前的策略概率分布，最后用梯度下降方
法来让最优策略的概率最大（这个算法称为策略梯度算法，Policy Gradient）

实际上，因为采样的输出结果是离散的，无法直接求导，所以不能使用反向传播的方法来优化网络，torch.distributions模块的存在目的就是为了解决这个问题，我们可以结合torch.distributions.Categorical进行采样，然后使用对数求导技巧来规避这个问题

当然，除了服从多项式分布的torch.distributions.Categorical类，PyTorch还支持其他的分布（包括连续分布和离散分布），比如torch.distributions.Normal类支持连续的正态分布的采样，可以用于连续的强化学习的策略

torch.hub模块

torch.hub提供了一系列预训练的模型供用户使用，比如，可以通过torch.hub.list函数来获取某个模型镜像站点的模型信息，然后通过torch.hub.load来载入预训练的模型，载入后的模型可以保存到本地，并可以看到这些模型对应类支持的方法

更多torch.hub支持的模型可以参考PyTorch官网中的相关页面

torch.jit模块

torch.jit是PyTorch的即时编译器（Just-In-Time Compiler，JIT）模块

这个模块存在的意义是把PyTorch的动态图转换成可以优化和序列化的静态图，其主要工作原理是通过输入预先定义好的张量，追踪整个动态图的构建过程，得到最终构建出来的动态图，然后转换为静态图（通过中间表示，即Intermediate Representation，来描述最后得到的图）

通过JIT得到的静态图可以被保存，并且被PyTorch其他的前端（如C++语言的前端）支持，另外，JIT也可以用来生成其他格式的神经网络描述文件，如ONNX

需要注意的一点是，torch.jit支持两种模式，即脚本模式（ScriptModule）和追踪模式（Tracing）

前者和后者都能构建静态图，区别在于前者支持控制流，后者不支持，但是前者支持的神经网络模块比后者少，比如脚本模式不支持torch.nn.GRU（详细的描述可以参考PyTorch官方提供的JIT相关的文档）

torch.multiprocessing模块

torch.multiprocessing定义了Pytorch中的多线程API，通过使用这个模块，可以启动不同的线程，每个进程运行不同的深度学习模型，并且能够在进程间共享张量（通过共享内存的方式）

共享的张量可以在CPU上，也可以在GPU上，多进程API还提供了与Python原生的多进程API（即multiprocessing库）相同的一系列函数，包括锁（Lock）和队列（Queue）等

torch.random模块

torch.random提供了一系列的方法来保存和设置随机数生成器的状态，包括使用get_rng_state函数来获取当前随机数生成器状态，set_rng_state函数设置当前随机数生成器状态，并且可以用manual_seed函数来设置随机种子

因为神经网络的训练是一个随机的过程，包括数据的输入，权重的初始化都具有一定的随机性，设置一个统一的随机种子可以有效地帮助我们测试不同结构神经网络的表现，有助于调试神经网络的结构

torch.onnx模块

torch.onnx定义了PyTorch导出和载入ONNX格式的深度学习模型描述文件

ONNX格式的存在是为了方便不同深度学习框架之间交换模型，引入这个模块可以方便PyTorch导出模型给其他深度学习框架使用，或者让PyTorch可以载入其他深度学习框架构建的深度学习模型

Pytorch的辅助工具模块

torch.utils提供了一系列的工具来帮助神经网络的训练，测试和结构优化，这个模块主要包括以下6个子模块

torch.utils.bottleneck模块

torch.utils.bottleneck可以用来检测深度学习模型中模块的运行时间，从而可以找到导致性能瓶颈的那些模块，通过优化特定模块的运行时间，从而优化整个深度学习模型的性能

torch.utils.checkpoints模块

torch.utils.checkpoints可以用来节约深度学习使用的内存

因为在训练的时候，需要进行梯度反向传播，所以在构建计算图的时候需要保存中间的数据，而这些数据会大幅增加深度学习的内存消耗

为了减少内存消耗，可以提高mini-batch的大小，从而提升深度学习模型的性能和优化时的稳定性，我们可以通过这个模块记录中间数据的计算过程，然后丢弃中间数据，需要调用的时候再重新进行计算

这个模块设计的核心思想就是以计算时间换内存空间

torch.utils.cpp_extension模块

torch.utils.cpp_extension定义了PyTorchC++扩展，其主要包含两个类

CppExtension定义了使用C++来编写的扩展模块的源代码相关信息，CUDAExtension则定义了C++/CUDA编写的扩展模块的源代码相关信息

在某些情况下，用户可能需要使用C++实现某些张量运算和神经网络结构（比如PyTorch没有类似功能的模块，或者PyTorch类似功能的模块性能比较低），PyTorch的C++扩展模块就提供了一个方法能够让Python来调用使用C++/CUDA编写的深度学习扩展模块

在底层上，这个扩展模块使用了pybind11,保持了接口的轻量性并使得PyTorch易于被扩展

torch.utils.data模块

torch.utils.data引入了数据集（Dataset）和数据载入器（DataLoader）的概念，前者包含了所有数据的数据集，通过索引能够得到某一条特定的数据，后者通过对数据集的包装，可以对数据集进行随机排（Shuffle）和采样（Sample），得到一系列打乱数据顺序的mini-batch

torch.utils.dlpacl模块

torch.utils.dlpacl模块定义了Pytorch张量和DLPack张量存储格式之间的转换，用于不同框架之间张量数据的交换

torch.utils.tensorboard模块

torch.utils.tensorboard模块是Pytorch对TensorBoard数据可视化工具的支持

TensorBoard原来是TensorFlow自带的数据可视化工具，能够显示深度学习模型在训练过程中损失函数、张量权重的直方图，以及模型训练过程中输出的文本、图像和视频等

TensorBoard的功能十分强大，而且是基于可交互的动态网页设计的，使用者可以通过预先提供的一系列功能来输出特定的训练过程的细节（如某一神经网络层的权重的直方图，以及训练过程中某一段时间的损失函数等）

Pytorch支持TensorBoard可视化之后，在Pytorch的训练过程中，可以很方便地观察中间输出的张量，也可以方便地调试深度学习模型

Pytorch张量介绍

张量的数据类型

张量常用的数据类型如下表所示

数据类型	CPU上的张量	GPU上的张量
32-bit floating point	torch.FloatTensor	torch.cuda.FloatTensor
64-bit floating point	torch.DoubleTensor	torch.cuda.DoubleTensor
16-bit floating point	torch.HalfTensor	torch.cuda.HalfTensor
8-bit integer (unsigned)	torch.ByteTensor	torch.cuda.ByteTensor
8-bit integer (signed)	torch.CharTensor	torch.cuda.CharTensor
16-bit integer (signed)	torch.ShortTensor	torch.cuda.ShortTensor
32-bit integer (signed)	torch.IntTensor	torch.cuda.IntTensor
64-bit integer (signed)	torch.LongTensor	torch.cuda.LongTensor
Bool	torch.BoolTensor	torch.cuda.BoolTensor

如果我们要获得一个张量的具体类型，可以访问张量的dtype属性，如果想要进一步获取张量的存储位置和数据类型，可以通过调用张量的type放阿飞来同时获得存储位置和数据类型的值，例如

import torch

my_tensor = torch.tensor([1, 2, 3, 4])

print(my_tensor)  # 转换Python列表为PyTorch张量
print(my_tensor.dtype)  # 查看张量数据类型
print(my_tensor.type)  # 查看张量具体情况

输出为

tensor([1, 2, 3, 4])
torch.int64
<built-in method type of Tensor object at 0x000001F05A6691D0>

注意：现阶段的Pytorch并不支持复数类型，如果有需要用到的地方，如使用torch.fft或torch.ifft进行快速傅里叶变换，则需要使用张量的两个分量来分别模拟复数的实部和虚部

在Pytoch的不同类型之间，可以调用to方法进行转换，该方法传入的参数是转换的目标类型，除此之外也可以直接调用相关的方法，例如

import torch

my_tensor = torch.tensor([1, 2, 3, 4])

print(my_tensor)  # 转换Python列表为PyTorch张量
print(my_tensor.dtype)  # 查看张量数据类型

# to方法转换
convert_tensor = my_tensor.to(torch.float32)
print(convert_tensor)
print(convert_tensor.dtype)
# 调用方法转换
other_tensor = my_tensor.float()
print(other_tensor)
print(other_tensor.dtype)

输出结果为

tensor([1, 2, 3, 4])
torch.int64
tensor([1., 2., 3., 4.])
torch.float32
tensor([1., 2., 3., 4.])
torch.float32

张量的创建

张量的创建主要有以下四种方法

1. 通过torch.tensor函数创建张量

例如

import torch

my_tensor = torch.tensor([1, 2, 3, 4], dtype=torch.int32)

print(my_tensor)  # 转换Python列表为PyTorch张量
print(my_tensor.dtype)  # 查看张量数据类型

输出为

tensor([1, 2, 3, 4], dtype=torch.int32)
torch.int32

2. 通过Pytorch内置的函数创建张量

import torch  # 导入torch包

torch.random.manual_seed(2024)

print(torch.rand(3, 3))  # 生成3×3的矩阵，矩阵元素服从[0, 1)上的均匀分布
print(torch.randn(2, 3, 4))  # 生成2×3×4的张量，张量元素服从标准正态分布
print(torch.zeros(2, 2, 2))  # 生成 2×2×2的张量，张量元素全为0
print(torch.ones(1, 2, 3))  # 生成1×2×3的张量，张量元素全为1
print(torch.eye(3))  # 生成3×3的单位矩阵
print(torch.randint(0, 10, (3, 3)))  # 生成0（包含）到10（不含）之间均匀分布整数的3×3矩阵

输出为

tensor([[0.5317, 0.8313, 0.9718],
        [0.1193, 0.1669, 0.3495],
        [0.2150, 0.6201, 0.4849]])
tensor([[[ 1.3891,  0.0495, -0.9902,  0.4790],
         [ 1.3130, -1.1611, -0.4426,  0.1236],
         [-1.4753, -1.4808,  0.0498,  1.2883]],

        [[-0.6491, -0.8969,  1.2634,  0.0306],
         [ 0.4594,  0.3922, -1.0767, -0.0576],
         [-0.0596,  0.2764, -0.2403,  0.3084]]])
tensor([[[0., 0.],
         [0., 0.]],

        [[0., 0.],
         [0., 0.]]])
tensor([[[1., 1., 1.],
         [1., 1., 1.]]])
tensor([[1., 0., 0.],
        [0., 1., 0.],
        [0., 0., 1.]])
tensor([[2, 9, 2],
        [2, 8, 2],
        [6, 4, 6]])

3. 通过已知张量创建形状相同的张量

还可以创建和已知张量形状相同的张量，但是里面填充的元素可能不一样，例如

import torch  # 导入torch包

torch.random.manual_seed(2024)

t = torch.randn(3, 3)  # 生成一个随机正态分布的张量t
print(t)
print(torch.zeros_like(t))  # 生成一个元素全为0的张量，形状和给定张量t相同
print(torch.ones_like(t))  # 生成一个元素全为1的张量，形状和给定张量t相同
print(torch.rand_like(t))  # 生成一个元素服从[0, 1)上的均匀分布的张量，形状和给定张量t相同
print(torch.randn_like(t))  # 生成一个元素服从标准正态分布的张量，形状和给定张量t相同

输出

tensor([[-0.0404,  1.7260, -0.8140],
        [ 1.3722,  0.5060, -0.4823],
        [-0.7853,  0.6681, -0.4439]])
tensor([[0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.]])
tensor([[1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.]])
tensor([[0.8914, 0.9090, 0.6652],
        [0.6786, 0.2268, 0.5031],
        [0.2151, 0.7988, 0.0784]])
tensor([[ 0.1888, -1.1668, -0.5003],
        [-1.0848, -0.5578, -1.1568],
        [-0.2284, -0.2605, -0.2314]])

4. 通过已知张量创建形状不同但数据类型相同的张量

也可以创建和已知张量数据类型相同的张量，但是形状可能不一样，例如

import torch  # 导入torch包

torch.random.manual_seed(2024)

t = torch.randn(3, 3)  # 生成一个随机正态分布的张量t

print(t)
print(t.new_tensor([1, 2, 3]))  # 根据Python列表生成张量，注意这里输出的是单精度浮点数
print(t.new_tensor([1, 2, 3]).dtype)  # 根据Python列表生成张量，注意这里输出的是单精度浮点数
print(t.new_zeros(3, 3))  # 生成相同类型且元素全为0的张量
print(t.new_ones(3, 3))  # 生成相同类型且元素全为1的张量

输出

tensor([[-0.0404,  1.7260, -0.8140],
        [ 1.3722,  0.5060, -0.4823],
        [-0.7853,  0.6681, -0.4439]])
tensor([1., 2., 3.])
torch.float32
tensor([[0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.]])
tensor([[1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.]])

其中，new_tensor方法用于创建张量，具体用法与torch.tensor方法类似，但是在这里新的张量的类型不再是torch.int64，而是和前面已知的张量的类型一致，为torch.float32

这种用法很少用到，一般用于写设备无关代码

需要注意的是，没有类似于new_rand和new_randn的函数，所以不能用这种方法生成随机元素填充的张量

张量的存储位置

Pytorch张量可以存储在两种设备上，即CPU和GPU，在没有指定的情况下，会默认存储在CPU上，如果要将张量存储到GPU上，需要指定张量转移到GPU设备

一般而言，GPU设备在Pytorch上以cuda:0、cuda:1$\cdots$指定，其中数字代表的是GPU（假设设备上挂载了$N$个GPU）的编号，范围是$0,1,2,\cdots,N-1$，关于GPU的详细信息可以用nvidia-smi命令查看，例如

Sun Jun 30 20:22:52 2024
+-----------------------------------------------------------------------------------------+
| NVIDIA-SMI 555.99                 Driver Version: 555.99         CUDA Version: 12.5     |
|-----------------------------------------+------------------------+----------------------+
| GPU  Name                  Driver-Model | Bus-Id          Disp.A | Volatile Uncorr. ECC |
| Fan  Temp   Perf          Pwr:Usage/Cap |           Memory-Usage | GPU-Util  Compute M. |
|                                         |                        |               MIG M. |
|=========================================+========================+======================|
|   0  NVIDIA GeForce RTX 3060 ...  WDDM  |   00000000:01:00.0  On |                  N/A |
| N/A   52C    P8             14W /   30W |       0MiB /   6144MiB |      0%      Default |
|                                         |                        |                  N/A |
+-----------------------------------------+------------------------+----------------------+

+-----------------------------------------------------------------------------------------+
| Processes:                                                                              |
|  GPU   GI   CI        PID   Type   Process name                              GPU Memory |
|        ID   ID                                                               Usage      |
|=========================================================================================|
|    No running processed found                                                           |
+-----------------------------------------------------------------------------------------+

对于前面1-3种的张量初始化方法，可以在创建张量的函数的参数中指定device参数来指定张量存储的位置，例如

import torch  # 导入torch包

torch.randn(3, 3, device="cpu")  # 获取存储在CPU上的一个张量
torch.randn(3, 3, device="cuda:0")  # 获取存储在0号GPU上的一个张量
torch.randn(3, 3, device="cuda:0").device  # 获取当前张量的设备
torch.randn(3, 3, device="cuda:0").cpu().device  # 张量从1号GPU转移到CPU

在控制台输入代码后，输出为

tensor([[-1.0908,  1.7492,  1.3315],
        [ 0.3292, -0.1265,  0.8655],
        [-0.6930,  0.3382,  0.6050]])
tensor([[-1.3110,  0.2978,  1.0934],
        [ 0.8837,  0.5539, -0.7756],
        [ 0.6421, -0.3814,  1.2210]], device='cuda:0')
device(type='cuda', index=0)
device(type='cpu')

可以通过访问张量的device属性获取张量所在的设备

如果想将张量从一个设备转移到另一个设备，有几种方法：可以使用cpu或cuda方法进行转移（cuda方法需要传入具体的GPU的设备编号），也可以使用to方法进行转移，该方法的参数是目标设备的名称（可以是字符串名称，也可以是torch.device实例）

注意：两个及以上数量的张量之间的运算只有在相同设备上才能进行（例如都在CPU上或者同一个GPU上），否则会报错

张量的维度

在深度学习中，我们经常会用到一些方法来获取张量的维度数目，以及某一维度的具体大小，或者对张量的某些维度进行操作

获取张量形状可以使用ndimension，size方法或shape属性，例如

import torch

t = torch.randn(3, 4, 5)  # 产生一个3×4×5的张量
print(t.ndimension())  # 获取维度的数目
print(t.nelement())  # 获取该张量的总元素数目
print(t.size())  # 获取该张量每个维度的大小，调用方法
print(t.shape)  # 获取该张量每个维度的大小，访问属性

输出为

3
60
torch.Size([3, 4, 5])
torch.Size([3, 4, 5])

除了获得张量的形状，我们有时候还需要对形状进行一定的修改，使之符合网络的结构或便于进行后续处理

一般有两种方法可以改变张量的形状，一个是view方法，另一个是reshape方法

先介绍view方法：view方法创建的张量会与原来的张量共享一个存储空间，也即意味着修改view创建的张量的值，原张量的值也会随之改变，例如

import torch  # 导入torch包

t = torch.randn(1, 2, 1)  # 产生一个3×4×5的张量
print(t)
b = t.view(2, 1, 1)
print(b)
b[1, 0, 0] = 0
print(b)
print(t)

输出为

tensor([[[-0.4887],
         [ 0.4076]]])
tensor([[[-0.4887]],

        [[ 0.4076]]])
tensor([[[-0.4887]],

        [[ 0.0000]]])
tensor([[[-0.4887],
         [ 0.0000]]])

可以看见修改b的值后，t的值也会随之改变

reshape方法与view方法类似，也是会使用共享内存，但是有一个前提：那就是原有的Tensor必须在读取时的物理存储顺序和逻辑读取顺序一致，否则会将原有数据重新复制一份到新的内存区，并使其存储顺序和读取顺序一致

此处可以去参考前文张量的存储位置和参考其他博客

简单来说，区别并不是很大，两者的最大不同点在于当存储顺序和逻辑顺序冲突时对内存的操作

张量的索引和切片

张量和Python的数组类似，也有切片和索引操作，例如

import torch  # 导入torch包

t = torch.randn(3, 2, 1)
print(t)
print(t[2, 1, 0])
print(t > 0)  # 得到BOOL掩码
print(t[t > 0])  # 根据掩码选取元素输出(最后结果的类型是tensor)
print(t[0:2, 0, 0])

输出为

tensor([[[-0.7896],
         [-0.9337]],

        [[ 1.4414],
         [ 1.1545]],

        [[-1.7856],
         [-2.0162]]])
tensor(-2.0162)
tensor([[[False],
         [False]],

        [[ True],
         [ True]],

        [[False],
         [False]]])
tensor([1.4414, 1.1545])
tensor([-0.7896,  1.4414])

Pytorch张量的运算

单个张量的函数运算

在深度学习的过程中，我们经常需要对张量进行各种运算，常见的运算如下所示

import torch  # 导入torch包

t = torch.rand(3, 4)
print(t)
print(t.sqrt())  # 等价于torch.sqrt(t)
t.sqrt_()  # 改变t原本的值
print(t)
print(t.mean())  # 等价于torch.mean()
print(t.mean(1))  # 对第1维的元素求平均
print(t.sum())  # 等价于torch.sum()
print(t.sum(0))  # 对第2维的元素求和

输出为

tensor([[0.5455, 0.1049, 0.7056, 0.9705],
        [0.7150, 0.3079, 0.4705, 0.1670],
        [0.4844, 0.8377, 0.1952, 0.8538]])
tensor([[0.7386, 0.3240, 0.8400, 0.9851],
        [0.8456, 0.5549, 0.6859, 0.4086],
        [0.6960, 0.9153, 0.4418, 0.9240]])
tensor([[0.7386, 0.3240, 0.8400, 0.9851],
        [0.8456, 0.5549, 0.6859, 0.4086],
        [0.6960, 0.9153, 0.4418, 0.9240]])
tensor(0.6966)
tensor([0.7219, 0.6238, 0.7443])
tensor(8.3598)
tensor([2.2802, 1.7941, 1.9677, 2.3178])

可以看出很多常用的数学运算函数都有两种调用方式，一种是调用张量自带的方法，另一种是调用torch包中的数学函数进行运算，二者是等价的，均返回一个新的张量

值得注意的是张量有一些内置的方法是带有_符号的，带有该下划线符号的方法会直接改变张量的值，这种操作称为“原地操作”

常用的原地操作有copy_，向这个方法内传入一个形状相同的张量，即可把这个张量的值复制到原张量中

不能直接使用=对张量进行赋值，否则会使两个张量绑定到同一个内存地址当中

此外，一些常用的函数例如torch.mean或torch.sum等，在进行计算时会自动消除被计算的维度，即给张量降维

如果需要保留维度，则需要设置参数keepdim=1

涉及多个张量的函数运算

多个张量之间也可以用函数进行运算，例如

import torch  # 导入torch包

t1 = torch.rand(2, 3)
t2 = torch.rand(2, 3)
print(t1)
print(t2)
print(t1.add(t2))
print(t1.sub(t2))
print(t1.mul(t2))
print(t1.div(t2))

输出为

tensor([[0.3407, 0.9995, 0.2602],
        [0.5217, 0.7332, 0.6589]])
tensor([[0.5516, 0.8645, 0.8194],
        [0.7578, 0.3524, 0.4786]])
tensor([[0.8924, 1.8640, 1.0795],
        [1.2796, 1.0857, 1.1375]])
tensor([[-0.2109,  0.1350, -0.5592],
        [-0.2361,  0.3808,  0.1804]])
tensor([[0.1880, 0.8641, 0.2132],
        [0.3954, 0.2584, 0.3153]])
tensor([[0.6177, 1.1562, 0.3175],
        [0.6885, 2.0805, 1.3769]])

同理，加了_的方法或函数会改变原张量的值

张量的极值和排序

一般我们需要寻找张量中的极值（最大值/最小值）时，我们可以使用argmax和argmin，即可返回极值所在的序号

若我们还需要极值的具体数值，我们还可以调用max和min，其会返回极值的位置和极值组成的元组（Tuple）

import torch  # 导入torch包

t = torch.randn(3, 4)
print(t)
print(t.argmax(0))  # 沿着第0个维度寻找
print(t.argmin(1))  # 沿着第1个维度寻找
print(t.min(1))  # 沿着第1个维度寻找
print(t.max())  # 全局最大值

输出为

tensor([[ 1.0603,  0.8296,  0.3234,  0.0555],
        [ 2.0685,  0.9660, -0.4212, -0.1690],
        [-0.9293, -0.2170, -0.3095,  1.7603]])
tensor([1, 1, 0, 2])
tensor([3, 2, 0])
torch.return_types.min(
values=tensor([ 0.0555, -0.4212, -0.9293]),
indices=tensor([3, 2, 0]))
tensor(2.0685)

在对张量内部元素进行排序的时候，我们常用sort函数，默认是升序排序

如果要改为降序排序，则需要设置参数descending=True

sort函数返回排序完成的张量以及对应排序后的元素在原始张量上的位置

import torch  # 导入torch包

t = torch.randn(3, 4)
print(t)
print(t.sort())

输出为

tensor([[-1.3162,  1.0094,  0.8514,  0.7259],
        [ 0.4570, -1.3140,  0.5615,  1.0809],
        [-1.8778,  2.0567, -2.1106, -0.2151]])
torch.return_types.sort(
values=tensor([[-1.3162,  0.7259,  0.8514,  1.0094],
        [-1.3140,  0.4570,  0.5615,  1.0809],
        [-2.1106, -1.8778, -0.2151,  2.0567]]),
indices=tensor([[0, 3, 2, 1],
        [1, 0, 2, 3],
        [2, 0, 3, 1]]))

矩阵的乘法和张量的缩并

张量之间除了基本的四则运算和普通数学运算之外，有时候还需要进行矩阵乘法（线性变换）

若输出的矩阵是二维的，则一般用torch.mm或张量内置的mm方法进行矩阵乘法的计算，有时候也会使用@运算符号实现（需要Python版本高于3.5），例如

import torch  # 导入torch包

a = torch.randn(3, 4)  # 建立一个3×4的张量
b = torch.randn(4, 3)  # 建立一个4×3的张量
print(torch.mm(a, b))  # 矩阵乘法，调用函数，返回3×3的矩阵乘积
print(a.mm(b))  # 矩阵乘法，内置方法
print(a @ b)  # 矩阵乘法，@运算符号

输出为

tensor([[ 0.3934,  4.7128, -2.6262],
        [-0.8621, -1.5481,  0.4649],
        [-3.7745, -8.1867,  6.8102]])
tensor([[ 0.3934,  4.7128, -2.6262],
        [-0.8621, -1.5481,  0.4649],
        [-3.7745, -8.1867,  6.8102]])
tensor([[ 0.3934,  4.7128, -2.6262],
        [-0.8621, -1.5481,  0.4649],
        [-3.7745, -8.1867,  6.8102]])

若输出的矩阵是三维的，则一般使用torch.bmm函数和bmm方法

在深度学习中，我们经常使用的是迷你批次的二维矩阵，所以两个三维的张量做矩阵乘法可以看做多个二维矩阵对应进行矩阵乘法，最后整合乘积的结果

例如$b\times m\times k$的张量和$b\times k\times n$的张量相乘，那么结果应该是一个$b\times m\times n$的张量

import torch  # 导入torch包

a = torch.randn(2, 3, 4)  # 建立一个大小为2×3×4的张量
b = torch.randn(2, 4, 3)  # 建立一个张量，大小为2×4×3
print(torch.bmm(a, b))  # 矩阵乘法，调用函数，返回3×3的矩阵乘积
print(a.bmm(b))  # 矩阵乘法，内置方法
print(a @ b)  # 矩阵乘法，@运算符号

输出为

tensor([[[ 0.1773,  0.4163,  2.6206],
         [-4.0776,  3.3618,  1.6795],
         [-0.7866,  2.5434, -1.3978]],

        [[-2.1043, -0.8359, -2.1261],
         [ 1.7787,  1.8698,  3.0646],
         [ 1.2775, -0.6378,  0.2742]]])
tensor([[[ 0.1773,  0.4163,  2.6206],
         [-4.0776,  3.3618,  1.6795],
         [-0.7866,  2.5434, -1.3978]],

        [[-2.1043, -0.8359, -2.1261],
         [ 1.7787,  1.8698,  3.0646],
         [ 1.2775, -0.6378,  0.2742]]])
tensor([[[ 0.1773,  0.4163,  2.6206],
         [-4.0776,  3.3618,  1.6795],
         [-0.7866,  2.5434, -1.3978]],

        [[-2.1043, -0.8359, -2.1261],
         [ 1.7787,  1.8698,  3.0646],
         [ 1.2775, -0.6378,  0.2742]]])

对于更高维度的张量的乘积，则需要决定各自张量元素乘积的结果合并的方向了，即看做小批次的降维矩阵乘法，相当于bmm的高维推广版，这个操作成为缩并

这个时候需要引入爱因斯坦求和约定

$$\pmb C_{ijki'j'k'\ldots} = \sum_{l_1l_2\ldots l_n}\pmb A_{ijk\ldots ml_1l_2\ldots l_n}\pmb B_{i'j'k'\ldots ml_1l_2\ldots l_n}$$

这里的下标分为三类：

• 在$\pmb{A\ B\ C}$中都出现的，意味着这两个下标对应的一系列元素需要做乘积（即张量积）
• 在$\pmb{A \ B}$中出现但是$\pmb C$中没有出现的，意味着这两个下标对应的一系列元素需要做乘积求和（类似于向量的内积）
• 在$\pmb{A\ B}$中出现，在$\pmb C$中只出现过一次且这两个指标对应的维度的大小相等，意味着这两个维度之间的元素按照位置做乘法

在上述条件下，前面的矩阵乘法和迷你批次矩阵乘法都能归结为爱因斯坦求和乘法，在Pytorch中对应的函数为torch.einsum

import torch  # 导入torch包

a = torch.randn(2, 3, 4)  # 随机产生张量
b = torch.randn(2, 4, 3)
print(a.bmm(b))  # 批次矩阵乘法的结果
print(torch.einsum("bnk,bkl->bnl", a, b))  # einsum函数的结果，和前面的结果一致

输出为

tensor([[[ 0.5561, -1.5121, -1.5252],
         [ 0.1253,  2.2359, -0.4644],
         [ 0.7896,  4.4894,  0.2480]],

        [[ 3.8017,  1.7904,  4.6185],
         [-1.4104,  2.7938,  0.3410],
         [ 0.2550,  4.1885,  2.4838]]])
tensor([[[ 0.5561, -1.5121, -1.5252],
         [ 0.1253,  2.2359, -0.4644],
         [ 0.7896,  4.4894,  0.2480]],

        [[ 3.8017,  1.7904,  4.6185],
         [-1.4104,  2.7938,  0.3410],
         [ 0.2550,  4.1885,  2.4838]]])

torch.einsum函数在使用的时候需要传入两个张量的下标对应的形状，以不同的字母来区分（字母可以任意选择，只需要服从前面的规则即可），以及最后输出张量的形状，用->符号连接，最后传入两个输入的张量，即可得到输出的结果

需要注意的是，求和的指标所在维度的大小一定要相同，否则会报错

张量的拼接和分割

在实际应用中，我们经常会对张量进行组合或者按一定形状进行分割，常用的有以下几个函数

• torch.stack函数的功能是指定并创建一个维度，然后将多个张量按照指定的维度进行堆叠拼接，并返回堆叠之后的张量，传入的张量的大小必须一致
• torch.cat函数指定某一个维度，将列表中的张量沿着该维度进行堆叠，并返回堆叠后的张量

torch.stack和torch.cat的区别是前者的维度一开始并不存在，需要先创建再拼接，而后者的维度是预先存在的，所有的张量都会沿着这个维度堆叠

• torch.split函数是将张量沿着指定的维度和大小进行分割
• torch.chunk函数与torch.split函数的功能类似，但是前者传入的参数是分割后的张量个数，而后者的参数是分割的片段大小

import torch  # 导入torch包

t1 = torch.randn(2, 3)  # 随机产生四个张量
t2 = torch.randn(2, 3)
t3 = torch.randn(2, 3)
t4 = torch.randn(2, 4)  # 沿着最后一个维度做堆叠，返回大小为3×4×3的张量
print(torch.stack([t1, t2, t3], -1).shape)
print(torch.cat([t1, t2, t3, t4], -1).shape)  # 沿着最后一个维度做拼接，返回大小为3×14的张量
t = torch.randn(3, 6)  # 随机产生一个3×6的张量
print(t)
print(t.split([1, 2, 3], -1))  # 把张量沿着最后一个维度分割为三个张量
print(t.split(3, -1))  # 把张量沿着最后一个维度分割，分割大小为3，输出的张量大小均为3×3
print(t.chunk(3, -1))  # 把张量沿着最后一个维度分割为三个张量，大小均为3×2

输出为

torch.Size([2, 3, 3])
torch.Size([2, 13])
tensor([[ 0.7721,  0.5936,  0.8516, -1.7305, -0.4206, -0.2412],
        [ 0.5102,  2.3383, -0.0702,  0.6323, -0.1546,  0.0466],
        [ 0.5990,  0.6999, -0.6723, -0.5615,  1.2148,  0.0053]])
(tensor([[0.7721],
        [0.5102],
        [0.5990]]), tensor([[ 0.5936,  0.8516],
        [ 2.3383, -0.0702],
        [ 0.6999, -0.6723]]), tensor([[-1.7305, -0.4206, -0.2412],
        [ 0.6323, -0.1546,  0.0466],
        [-0.5615,  1.2148,  0.0053]]))
(tensor([[ 0.7721,  0.5936,  0.8516],
        [ 0.5102,  2.3383, -0.0702],
        [ 0.5990,  0.6999, -0.6723]]), tensor([[-1.7305, -0.4206, -0.2412],
        [ 0.6323, -0.1546,  0.0466],
        [-0.5615,  1.2148,  0.0053]]))
(tensor([[0.7721, 0.5936],
        [0.5102, 2.3383],
        [0.5990, 0.6999]]), tensor([[ 0.8516, -1.7305],
        [-0.0702,  0.6323],
        [-0.6723, -0.5615]]), tensor([[-0.4206, -0.2412],
        [-0.1546,  0.0466],
        [ 1.2148,  0.0053]]))

张量维度的扩增与压缩

有时候因为一些特殊需要，我们会给张量增加或压缩维度

为了不引起数据的缺失，这种维度的操作一般针对大小为$1$的维度，因为这样也不会改变张量的大小

import torch  # 导入torch包

t = torch.rand(3, 4)  # 随机生成一个张量
print(t.shape)
print(t.unsqueeze(-1).shape)  # 扩增最后一个维度
print(t.unsqueeze(-1).unsqueeze(-1).shape)  # 继续扩增最后一个维度
print(t.squeeze().shape)  # 压缩所有大小为1的维度

输出为

torch.Size([3, 4])
torch.Size([3, 4, 1])
torch.Size([3, 4, 1, 1])
torch.Size([3, 4])

张量的广播

在运算中有时候会碰到一种情况：即两个不同维度的张量之间进行四则运算，且这两个张量的某些维度是相等的

显然如果我们遵照张量的运算规则，这两个张量是无法进行运算的，所以为了能够进行运算，首先需要把维度比较小的张量扩增到和维度数目比较大的张量一致，且能够在维度上对齐

一般存在两种情况：一种是至少有一个张量的对应维度大小为$1$，另一种是两个维度大小均不为$1$，但是相等

假设一个张量的大小为$3\times4\times5$，另外一个张量大小为$3\times5$，为了能够让两个张量进行四则运算，需要把第二个张量的形状展开成$3\times1\times5$，这样两个张量就能对齐

我们再将$3\times1\times5$的张量沿着第二个维度复制$4$次，使之成为$3\times4\times5$的张量，这样这两个张量就能进行计算了

import torch  # 导入torch包

t1 = torch.rand(3, 4, 5)  # 定义3×4×5的张量1
t2 = torch.rand(3, 5)  # 定义 3×5的张量2
print(t1)
print(t2)
t2.unsqueeze_(1)  # 张量2的形状变为3×1×5
print(t1.shape)
print(t2.shape)
t3 = t1 + t2  # 广播求和，最后结果为3×4×5的张量
print(t3)
print(t3.shape)

输出为

tensor([[[0.7498, 0.2657, 0.5337, 0.1923, 0.2748],
         [0.7335, 0.3172, 0.1872, 0.4740, 1.0000],
         [0.8014, 0.9461, 0.6369, 0.3823, 0.1218],
         [0.6268, 0.5680, 0.0517, 0.0586, 0.4711]],

        [[0.4524, 0.8449, 0.5609, 0.3580, 0.8733],
         [0.2869, 0.1558, 0.2796, 0.5478, 0.7139],
         [0.8551, 0.0787, 0.7032, 0.9882, 0.8096],
         [0.1838, 0.0476, 0.0375, 0.4214, 0.7748]],

        [[0.4135, 0.9216, 0.2737, 0.0055, 0.1296],
         [0.3005, 0.9491, 0.1710, 0.1161, 0.4242],
         [0.3991, 0.8930, 0.1317, 0.3849, 0.2975],
         [0.0131, 0.1442, 0.1009, 0.6065, 0.1295]]])
tensor([[0.8183, 0.6600, 0.9113, 0.2743, 0.6280],
        [0.4389, 0.5120, 0.3687, 0.3260, 0.7206],
        [0.4537, 0.5275, 0.5280, 0.1007, 0.3641]])
torch.Size([3, 4, 5])
torch.Size([3, 1, 5])
tensor([[[1.5681, 0.9257, 1.4450, 0.4666, 0.9028],
         [1.5518, 0.9772, 1.0984, 0.7483, 1.6280],
         [1.6197, 1.6062, 1.5482, 0.6566, 0.7498],
         [1.4451, 1.2280, 0.9630, 0.3329, 1.0991]],

        [[0.8913, 1.3568, 0.9295, 0.6840, 1.5939],
         [0.7258, 0.6678, 0.6483, 0.8738, 1.4345],
         [1.2940, 0.5907, 1.0719, 1.3142, 1.5302],
         [0.6227, 0.5596, 0.4062, 0.7474, 1.4954]],

        [[0.8673, 1.4492, 0.8017, 0.1061, 0.4937],
         [0.7543, 1.4767, 0.6990, 0.2167, 0.7883],
         [0.8528, 1.4206, 0.6597, 0.4856, 0.6616],
         [0.4669, 0.6718, 0.6289, 0.7072, 0.4936]]])
torch.Size([3, 4, 5])