信号处理基础
平滑窗
锐化窗或平滑窗是一个从中心峰值点向两侧衰落的实函数,在信号处理中用来缓解有限长度信号的截断影响
由于加窗具有使孔径中心的权值高于两端权值的效应,故又称“加权”
旁瓣的降低会导致分辨率的展宽,所以需要折中考虑
在脉冲压缩中,常使用窗来控制旁瓣,同时保持尽可能高的分辨率,一般使用Kaiser窗
Kaiser窗
在时域中,长度为T的Kaiser窗可以表示为
wk(t,T)=I0(β)I0(β1−(2t/T)2),−2T≤t≤2T
其中β是可以调整的衰减系数或平滑系数,I0为零阶贝塞尔函数
Kaiser窗的傅里叶变换或傅里叶逆变换为一个sinc函数
当β=0时,Kaiser窗退化成矩形窗;当β>0时,随着β的增大,峰值旁瓣比将会减小,3dB宽度将会扩大
其他窗
另外常用的窗是Hanning窗和Hamming窗,其时域表达式为
wh(t,T)=α−(1−α)cos(T2πt),−2T≤t≤2T
Hanning窗的α=0.5,称为余弦平方窗;Hamming窗的α=0.54,称为升余弦平方窗
当α可改变时,上式称为广义余弦窗,α可用于控制平滑度
插值
在许多场合中,我们需要知道信号在其他非整数点上的值,此时就需要通过插值实现重采样
非整数点上的信号可以通过DFT的平移/调制性质或频域补零得到
但是前者只能得到一定偏移后的初始信号采样点,后者仅能得到间隔为M1的采样点,其中M是扩展系数(必须是整数)
所以我们需要使用卷积实现插值,且需要选择尽可能高效准确的插值因子,公式如下所示
g(x)=i∑gd(i)h(x−i)
其中h(x)称为插值因子或插值核,在实际应用中,核是x的偶函数,故有h(x−i)=h(i−x)
i处的样本被核h(x−i)加权,插值点x处的g(x)等于插值核内的样本gd(i)与h(x−i)的乘积之和,即g(x)等于x邻域样本的加权和
sinc插值
sinc插值的卷积核是sinc函数
h(x)=sinc(x)=πxsin(πx)
插值信号为
g(x)=i∑gd(i)sinc(x−i)
为了重建信号g(x),我们只需要一个周期的频谱(如基带周期),因此需要理想矩形低通滤波器在频域中提取基带频谱
易知理想低通滤波器在时域中是一个sinc函数,频域相乘相当于时域卷积,所以插值可以通过和sinc核卷积实现
为了获取某一点处的精确值,卷积核需要覆盖无限多个点,实际上这是不可能的
我们在应用中常常会截断卷积核
需要注意的是,我们在截断卷积核之后,需要进行归一化处理,否则采样点上的权值和不再等于1,并且在不同插值点处会存在差异
归一化之后的插值结果应该是
g′(x)=Sg(x)
其中S是在特定插值点处的权值和
S=i∑sinc(x−i)
其中i受限于核的尺寸,对于需要恒定信号功率的情况,归一化常数为
S2=i∑sinc2(x−i)
随着核长的增加,两种情况的归一化常数逐渐接近于1,其区别相应减小
归一化权值的和(或平方和)为1
加窗的sinc函数
当使用截断的sinc核对存在陡峭边缘的函数进行插值时,会出现一种称为Gibbs效应的振铃现象
为了减小这种影响,我们需要对插值核进行锐化窗加权
无论核有多长,都存在振铃现象
振铃可以通过加窗来压低,但是代价是带宽的进一步损失
在实际应用中很少采用长度超过16的核,一个8点的加权sinc函数比较适用于SAR处理
非基带插值
当需要插值的频段不是基带时,我们有两种方法可以实现插值
- 将信号移至基带
- 将基带滤波器移至信号中心频率处
脉冲压缩
线性调频信号
线性调频信号的时域和频域表达式
在时域中,一个理想的线性调频信号或脉冲的持续时间为T秒,振幅为常量,中心频率为fcenHz,相位θ(t)随时间按一定规律变化
由于频率是线性调制的,相位是时间的二次函数,当fcen=0时,信号的复数形式为
g(t)=rect(Tt)exp(jπKt2)
其中t是时间变量,单位是秒,K是线性调频率,单位是Hz/s
对于实信号而言,带宽(Bandwidth)指的是chirp斜率及其持续时间的乘积
BW=∣K∣T
后续将指出,带宽决定了能够达到的分辨率
另一个重要的参数为时间带宽积(TBW),它是带宽和chirp持续时间T的乘积,该参数是无量纲的,为
TBP=∣K∣T2
此处省略证明得到线性调频信号的频谱为
G(f)=rect(KTf)exp(−jπKf2)
线性调频信号的采样
对于一个复线性调频信号,其最高频率应为∣K∣T/2(即带宽的一半),所以最低的复采样率fs应该大于带宽∣K∣T
定义过采样因子为
αOS=∣K∣Tfs
通常为了有效的利用数据采样点,又能留有足够的频谱间隙,过采样因子一般选择在1.1~1.4之间
脉冲压缩
脉冲压缩原理
不妨设发射脉冲的持续时间为T,则压缩前的可分辨能力为
ρ′=T
在任意时刻,回波中间隔大于这一时间的两个目标都不会被同一脉冲同时照射到,因此为了良好的分辨率,必须使用短脉冲或经过处理能得到短脉冲的信号
但是为了得到精确的目标参数,接收信号的SNR必须足够高,这一要求经常与分辨率相矛盾
脉冲压缩解决了这个矛盾,可以通过发射一个展宽脉冲,再对其进行脉冲压缩以得到所需分辨率
因此,为了取得好的脉冲压缩,必须对接收信号进行处理,使其频谱幅度非常平坦,相位仅包含常量和线性分量
频域中的脉冲压缩本质上是将信号频谱与含有二次共轭相位的频域滤波器进行相乘
脉冲压缩又称为“匹配滤波”
时域压缩
不妨设发射的信号为线性调频信号,则经过t0时延后的目标接收回波可表示为
sr(t)=rect(Tt−t0)exp{jπK(t−t0)2}
当t0=0时,匹配滤波器为时间反褶之后s(t)的复共轭
h(t)=rect(Tt)exp(−jπKt2)
匹配滤波器的输出近似为sinc函数
sout(t)≈Tsinc(KT(t−t0))
当时宽带宽积较大时,近似较为精确
脉冲分辨率
分辨率指压缩后信号中的两个-3dB点之间的间隔,其为幅度峰值0.707倍处的脉冲宽度
由于∣K∣T为带宽,分辨率为带宽的倒数,即
ρ=∣K∣T0.886≈∣K∣T1
在某些情况下,0.886可以近似忽略不计,尤其是考虑加窗引入的展宽影响时
带宽越大,分辨率越高
分辨率又称冲激响应宽度(IRW)
匹配滤波器的生成
- 将时间反褶之后的复制脉冲(发射复制脉冲)取复共轭,计算补零DFT
- 复制脉冲补零后进行DFT,对结果取复共轭(无时间反褶)
- 根据设定的线性调频性质,直接在频域生成匹配滤波器
如果调频率失配,则压缩结果的误差将会很大
合成孔径的概念
术语定义
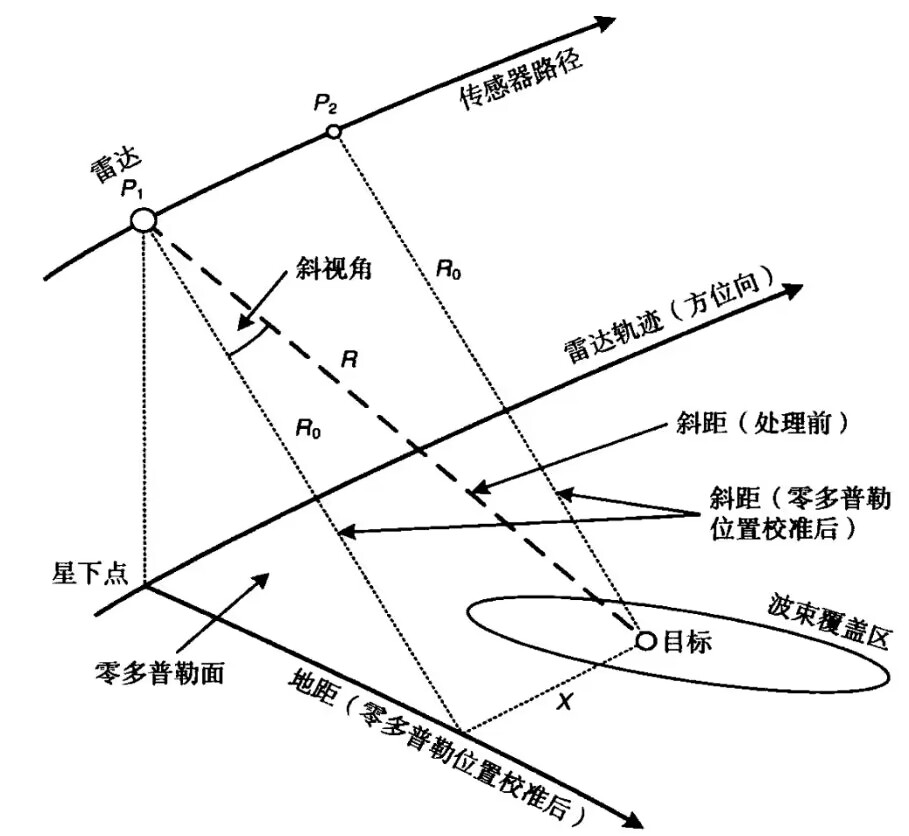
目标:这是被SAR照射的地球表面上的一个假想点,一般称为点目标或点散射体
波束覆盖区:随着发射平台的前移,具有电磁能量的脉冲以一定的间隔向地面发射,在某个脉冲的发射过程中,雷达天线的波束投影到地面的某个区域,称其为波束覆盖区,又称雷达波束照射区域
星下点:星下点是指直接位于传感器下方的地表点,所以星下点至传感器的连线是地球表面的法线
在地球圆球模型下,传感器至地心的矢量与地球表面相交于星下点;但在椭球模型下并非如此
雷达轨迹:星下点在地球表面上的移动轨迹
速度:
- 平台速度:平台沿飞行路径的速度,用Vs表示
- 波束速度:指零多普勒线扫过地面的速度,用Vg表示
方位向:在SAR处理中,该方向与平台相对速度矢量一致
零多普勒面:指一个垂直于平台速度矢量的包含传感器的平面,它近似垂直于方位坐标轴(因为可能平台存在起伏)。这个平面与地面之间的交线称为零多普勒线,当此线经过目标时,传感器相对于目标的径向速度为0
最短距离:随着平台的移动,雷达到目标的距离是随时间变化的,当距离达到最小值的时候(即零多普勒线经过目标时),称为最短距离,图中用R0表示
最近距离:最近距离指的是雷达距离物体最近的位置
由于波束的斜视,当传感器处于这个位置时,目标不一定能被照射到
零多普勒时刻:指传感器与目标最接近的时刻
波束宽度:雷达波束可以看作是一个圆锥体,而波束覆盖区为圆锥体与地面相切形成的截面。雷达波束有两个重要量度:方位平面内的角宽和俯仰平面内的角宽。在每个平面内的半功率波束宽度由波束“边缘”角界定。波束边缘由辐射强度处于峰值以下3dB处的位置来定义
目标轨迹:在雷达波束的照射时间内,雷达到目标的距离是不停变化的,表现在由距离和方位构成的二维图上,则为接收到的目标能量沿曲线分布,称其为信号空间内的目标轨迹
波束中心穿越时刻:波束中心线穿越目标的时刻与零多普勒线穿越目标的时刻不同,它有时候也称波束中心偏移时间
对于单极雷达而言是重合的
距离:首先,距离一般指的是斜距或者地距,前者沿着雷达视线方向测量,后者沿着地面测量。如果不加特殊说明,则距离一般默认为斜距
斜距平面:对于一个特定的目标,这个平面包含了传感器相对速度矢量和斜距矢量,对于不同距离R0上的目标,该平面与本地垂线的夹角也是不同的
地距:指斜距在地面上的投影,其原点在星下点
斜视角:斜视角θsq是斜距矢量与零多普勒面之间的夹角,是在斜距平面测量的,对于一个特定的波束指向,斜视角依赖于目标距离R0
目标的零多普勒时刻和斜视角无关,但是波束中心穿越时刻依赖于斜视角
距离横向:指与雷达视线正交的方向
除非斜视角为0,否则距离横向和方位向并不平行,但是由于斜视角通常很小,距离横向分辨率和方位分辨率没有明显区别
SAR距离向信号
发射脉冲
在距离向,雷达发射的调频脉冲为
spul(τ)=wr(τ)cos(2πn=0∑NPnτn)
其中,τ为距离向时间,Pn是当信号相位以幂级数表示时的相位系数
脉冲包络通常可以近似为矩形
wr(τ)=rect(Trτ)
其中Tr为脉冲持续时间
最常用的脉冲是具有线性调频特性的脉冲
spul(τ)=wr(τ)cos{2πf0τ+πKrτ2}
其中Kr为距离向脉冲的调频率,为简便起见,τ以脉冲中心为参考原点
在这种形式中,相位系数为P0=0,P1=f0,P2=Kr/2以及Pn=0,n>2
信号spul(τ)的瞬时频率随快时间τ变化,对于线性调频脉冲,瞬时频率为fi=f0+Krτ
由于雷达的波长为c/fi,因而脉冲之内的波长也是变化的,但是变化并不是很明显
如无特殊说明,则波长λ指的就是中心频率的波长,λ=c/f0
数据获取
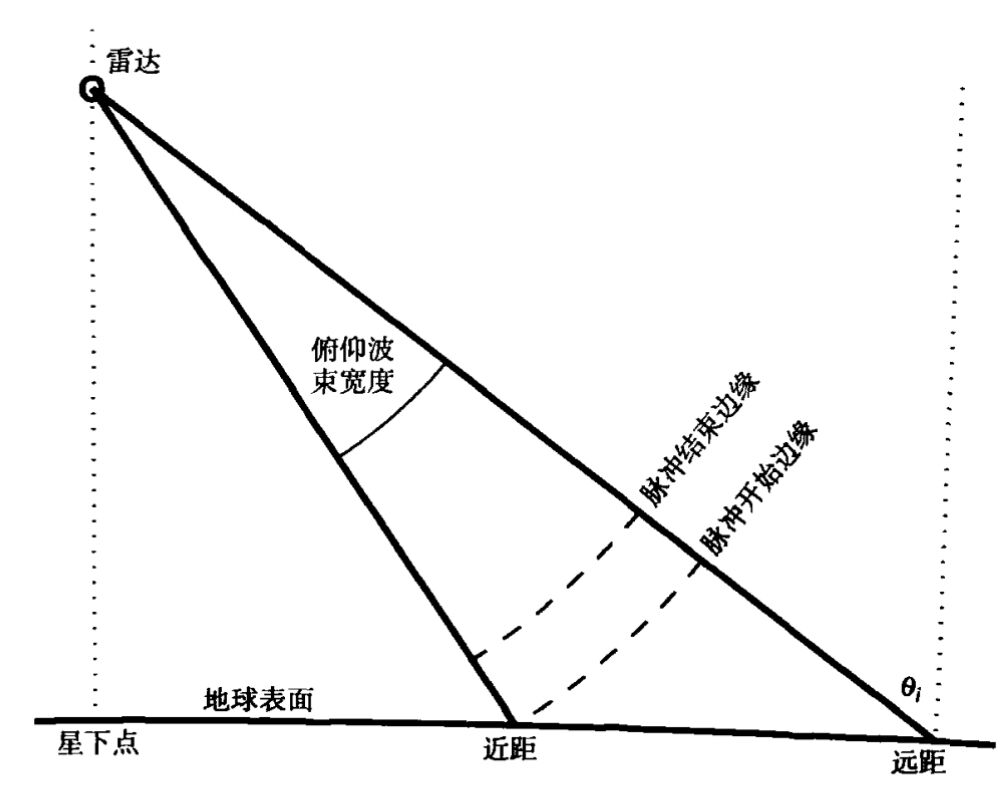
上图表示了距离条带内的数据是如何获取的
雷达波束在俯仰平面内具有一定的3dB宽度,称为俯仰波束宽度,在某一特定时刻,脉冲范围由图中两条虚线圆弧限定
脉冲以光速沿着同心球面向外传播,图中位于下方的虚线圆弧表示脉冲从天线发射后经过时间t1到达地面,在不到1ms后的t2,脉冲结束边缘经过远距点
这样,近距点和远距点之间的每个点都被波束持续照射了Tr
但是在任一时刻,只有部分波束覆盖区被脉冲照射,并且该区域以sinθic的速度向外推进
其中θi为本地波束入射角,任一照射时刻的反射能量是脉冲波形和照射区域内地面反射系数gr的卷积,即
sr(τ)=gr(τ)⨂spul(τ)
反射能量在2t1~2t2时间段内回到雷达接收天线
和脉冲间隔相比,如果俯仰波束显得过宽,则会出现距离模糊,这是由于来自连续相邻脉冲的反射能量在接收机处的混叠引起的
考察距雷达Ra处的一个点目标,其后向散射系数σ0的幅度为A0′,则可得gr(τ)=A0′δ(τ−2Ra/c),其中2Ra/c为该点信号的延时
可得该点目标的接收信号为
sr(τ)=A0′wr(τ−2Ra/c)×cos{2πf0(τ−2Ra/c)+πKr(τ−2Ra/c)2+ψ}
其中,ψ表示地表散射过程可能引起的雷达信号的相位改变,对于特定的反射体,只要在雷达照射时间内其相位变化为常数,前述分析就仍然适用
回波sr(τ)包含了一个反映雷达载频的高频分量cos(2πf0τ)和由上式剩余部分组成的低频分量
可以通过正交解调的方法去除高频分量,以使得信号的最大频率点在发射脉冲带宽内
SAR方位向信号
PRF的选择
- 奈奎斯特采样率:由于是复采样,PRF应大于方位信号带宽的主要部分。方位向过采样率αos,a一般为1.1~1.4。如果PRF太低,由混叠引起的方位模糊会很严重。
方位向过采样率通常大于距离向过采样率,因为方位频谱比距离频谱衰落得慢
-
距离测绘带宽度:采样窗时间上限为1/PRF−Tr秒,相应的斜距间隔为(1/PRF−Tr)c/2 m。PRF必须足够低以使处于波束照射范围内的所有近距至远距的回波信号都落在接收窗里面。如果PRF相对于回波持续时间过大,由于不同脉冲的回波在接收窗内重叠在一起,则会产生距离模糊。如果距离模糊过大且PRF不能降低,就需要通过增加天线宽度或调整天线权值的方法来减小天线在俯仰面内的波束宽度
-
接收窗时序:大部分地面反射能量必须在脉冲间隔内被天线接收
-
星下点回波:有时来自于星下点处的地面反射能量会比较大,导致图像上出现亮条纹。这是因为星下点的入射角小,每个距离单元覆盖了较大面积并且发生的是镜像反射,所以星下点回波比较亮。因为星下点回波也是距离模糊,因而这一能量是星载SAR应尽量避免的,通常会选择合适的PRF,使得星下点回波不落在接收窗之内
方位向信号强度和多普勒历程
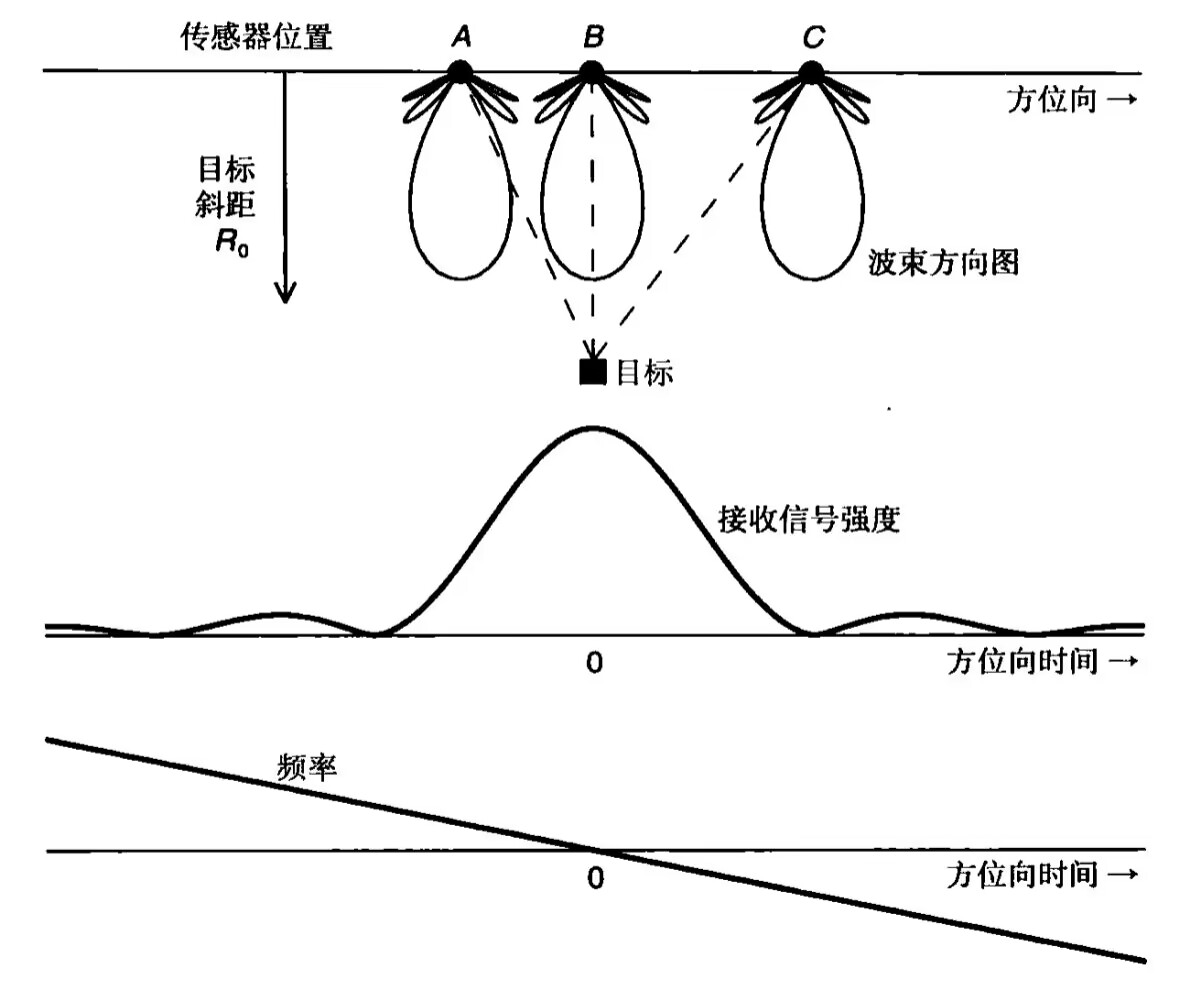
随着平台的前进,地面上的某个目标被数百个脉冲照射
主要由于方位向波束方向的影响,每个脉冲的回波信号强度存在变化,上图以斜距平面内的三个传感器位置为例,示意了正侧视情况下的方位向波束方向图
当传感器处于A点时,目标刚刚进入波束主瓣,其接收信号的强度如图中所示
在目标被波束中心(图中B点)照射之前,接收信号强度一直不断增加
当波束中心穿过目标时,在目标被波束方向图的第一个零点(图中的C点)照射到之前,信号强度又逐渐减弱,此后仍然可以接收到来自波束方向图副瓣的少许能量
波束方向图主瓣外沿以及副瓣的接收能量会造成图像中出现方位模糊,而多普勒中心频率的估计误差则会加重这些模糊
图中的下半部分也示意了目标的多普勒历程,多普勒频率正比于目标相对于传感器的径向速度
当目标接近雷达时多普勒频率为正,当目标远离雷达时多普勒频率为负,因此频率随时间的变化曲线的斜率为负
由上图中的中图可知,接收信号强度由方位向波束方向图决定,由于绝大多数SAR天线在方位面内都没有加权,其单程方向图可以近似为一个sinc函数
pa(θ)≈sinc(βbw0.886θ)
其中θ为斜距平面内测得的与视线的夹角,βbw为方位向波束宽度0.886λ/La,La为方位向天线长度
由于雷达能量的双程传播特征,接收信号的强度由pa(θ)的平方给出,并且通常可以表示为方位时间η的函数
wa(η)=pa2{θ(η)}
传感器到目标点的距离R(η)由如下等式给出
R2(η)=R02+Vr2η2
其中R0为雷达距离目标最近时的斜距,即最短距离,Vr是飞机的设计时速
基于上述讨论,可以推得点目标接收信号的表达式
sr(τ,η)=A0wr(τ−2R(η)/c)wa(η−ηc)×cos{2πf0(τ−2R(η)/c)+πKr(τ−2R(η)/c)2+ψ}
通常SAR数据在方位频域进行处理,即波束中心穿越时刻等效转换成频域中的多普勒中心频率
方位向参数
多普勒中心频率
η=ηc处的多普勒中心频率正比于前式中R(η)的变化率,量纲为Hz
fηc=−λR(ηc)2Vr2ηc=λ2Vrsinθr,c
多普勒中心频率也可以通过卫星实际速度Vs和实际斜视角θsq,c来表示
fηc=λ2Vssinθsq,c
其中Vssinθsq,c为雷达至目标视线方向上的径向速度,且Vs是定义在ECR坐标系下的
多普勒带宽
目标的方位向带宽为
Δfdop=λ2Vscosθr,cθbw=0.886La2Vscosθr,c
其中Vs为卫星的切向速度
该等式利用了一个事实:带宽是目标在雷达3dB波束(θbw=0.886λ/La)照射期间产生的频率漂移
这一带宽决定了采样要求,即确定了PRF的下限
一般而言,过采样率取为1.1~1.4,PRF设为过采样率和Δfdop的乘积
目标照射时间
照射时间是目标处于3dB波束范围内的时间宽度,可写为
Ta=0.886LaVgcosθr,cλR(ηc)
上式中0.886λ/La为方位向波束宽度,因此0.886R(ηc)λ/La为该波束在地面上的投影,Vg为波束覆盖区沿着地面的移动速度
在斜视角不为0的情况下,投影长度还需要乘以系数1/cosθr,c
方位向调频率
方位向调频率是方位向频率或多普勒频率的变化率
Ka=λR02Vr2cos3θr,c
其中方位向调频率为λ2乘以距离的一阶导数
如果是机载SAR,Vg=Vr=Vs
解调后的基带信号
接收信号sr包含了雷达载频cos(2πf0τ),在采样之前,载频必须通过正交解调过程予以去除
解调后单个点目标的基带信号可以表示为复数形式
s0(τ,η)=A0wr(τ−2R(η)/c)wa(η−ηc)×exp{−j4πf0R(η)/c}exp{jπKr(τ−2R(η)/c)2}
其中系数A0为一个复常数
A0=A0′exp(jψ)
其中A0′为点目标的后向散射系数的幅度
SAR冲激响应
如果忽略A0,则上式可写为单位幅度点目标的冲激响应,因而SAR传感器的冲激函数可以表示为
himp(τ,η)=wr(τ−2R(η)/c)wa(η−ηc)×exp{−j4πf0R(η)/c}exp{jπKr(τ−2R(η)/c)2}
为了建立地面接收信号的一般模型,将地面反射率与该冲激响应进行二维卷积,从而得出SAR基带信号数据为
sbb(τ,η)=g(τ,η)⨂himp(τ,η)+n(τ,η)
其中n(τ,η)为实际系统中的附加噪声,可以用高斯白噪声来建模
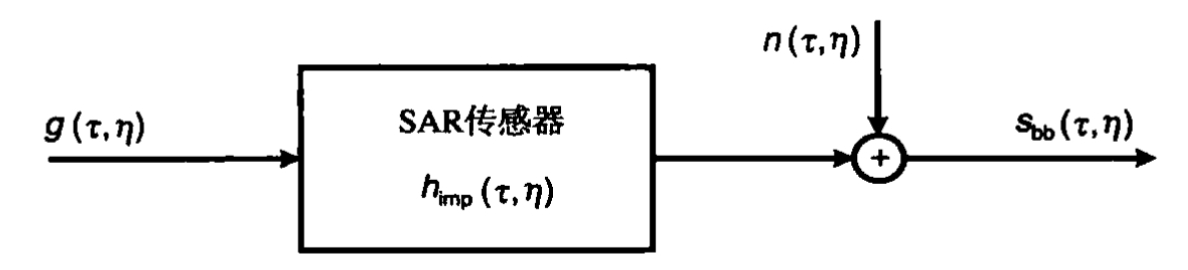
在仿真实验中,为了观察所用的匹配滤波器的功率相对于噪声基底的突出程度,最好将噪声包含进去
下图为机载和星载SAR雷达的典型参数
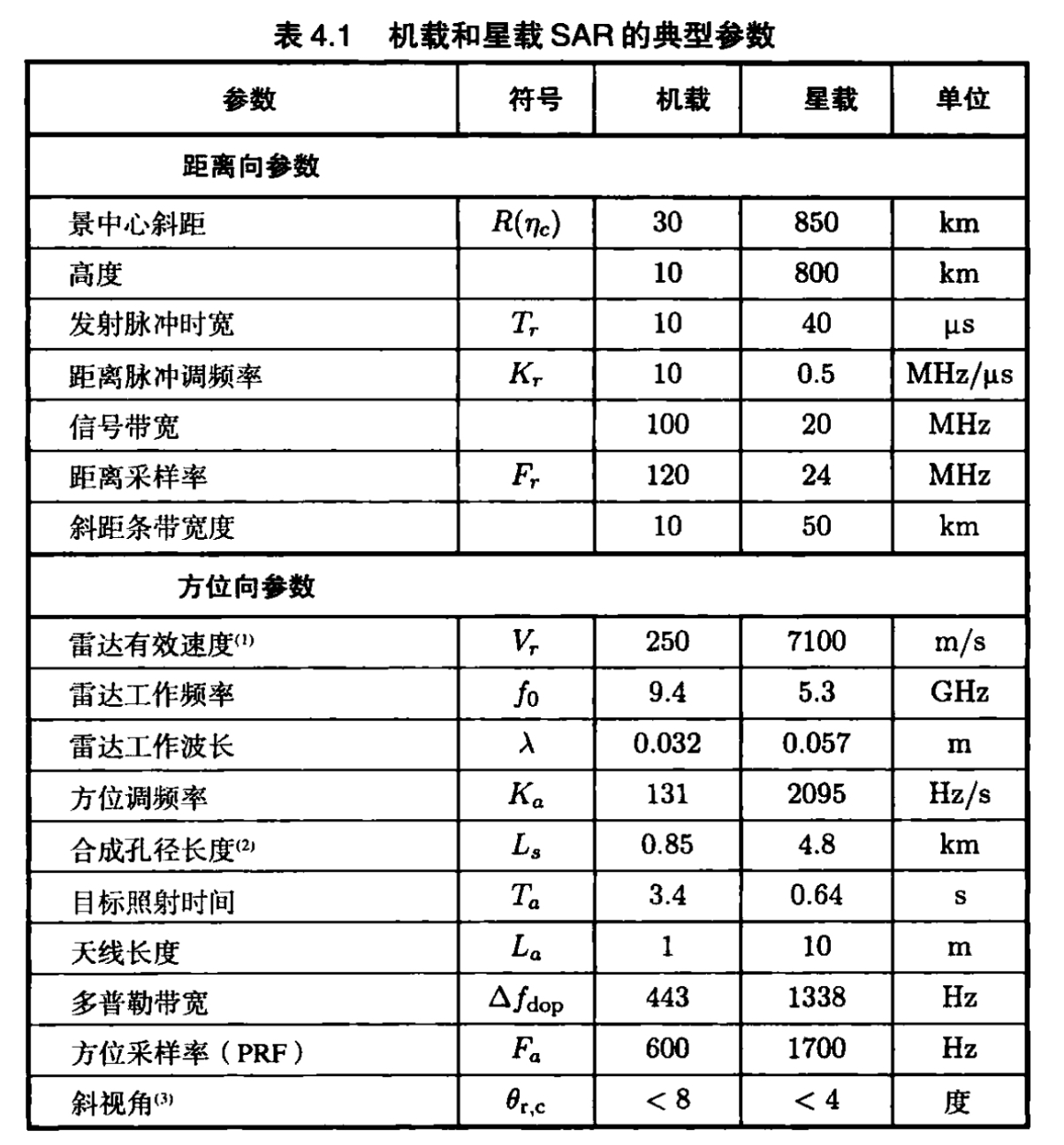
成像算法
如无特殊说明,仿真的环境均为MATLAB R2023a
回波产生
如无特殊说明,下列成像算法的仿真均是对此回波进行处理
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
|
clc,clear,clf;
c = 3e8;
pi = 3.1415926;
j = sqrt(-1);
f_radar = 5.3e9;
lamda = c / f_radar;
theta = 2 / 180 * pi;
R0_cen = 2e4;
R0 = R0_cen * cos(theta);
Tr = 2.5e-6;
Bw = 5e7;
Kr = Bw / Tr;
alpha = 3.4;
Fr = alpha * Bw;
V_radar = 150;
La = 3.75;
Bw_dop = 2 * V_radar * cos(theta) / La;
beta = 2.5;
PRF = beta * Bw_dop;
Ka = 2 * V_radar .^ 2 * (cos(theta)) .^ 3 / lamda / R0;
Ts = Bw_dop / abs(Ka);
Ls = V_radar * Ts;
f_eta_cen = 2 * V_radar * sin(theta) / lamda;
wave_width = 0.886 * lamda / La;
obj_list = [
R0 ,R0 * tan(theta) ,1,1
R0 + 50 ,R0 * tan(theta) + 100 ,1,1
R0 + 150,R0 * tan(theta) + 100 * tan(theta) + 100,1,1
];
delta_x = max(obj_list(:,1)) - min(obj_list(:,1));
delta_y = max(obj_list(:,2)) - min(obj_list(:,2));
obj_num = find(obj_list(:,4) == 1);
eta_c = zeros(length(obj_num),1);
for i = 1:length(obj_num)
eta_c(i) = (obj_list(obj_num(i),2) - obj_list(obj_num(i),1) * tan(theta)) / V_radar;
end
Nr = 2 ^ nextpow2((2 * (delta_x / c) + Tr) * Fr);
tau = 2 * R0 / c + linspace(-Nr / 2 / Fr,Nr / 2 / Fr,Nr);
f_tau = linspace(-Fr / 2,Fr / 2,Nr);
dr = c / 2 .* tau;
Na = 2 ^ nextpow2((delta_y + 2 * Ls) / V_radar * PRF);
t_eta = linspace(-Na / 2 / PRF,Na / 2 / PRF,Na);
f_eta = f_eta_cen + linspace(-PRF / 2,PRF / 2,Na);
tau_2d = ones(Na,1) * tau;
f_tau_2d = ones(Na,1) * f_tau;
t_eta_2d = t_eta' * ones(1,Nr);
f_eta_2d = f_eta' * ones(1,Nr);
echo = zeros(Na,Nr);
for k = 1:length(obj_num)
Rn = sqrt((obj_list(obj_num(k),1) .* ones(Na,Nr)) .^ 2 + (V_radar .* t_eta_2d - obj_list(obj_num(k),2) .* ones(Na,Nr)) .^ 2);
wr = (abs(tau_2d - 2 .* Rn / c)) <= ((Tr / 2) .* ones(Na,Nr));
theta_wa = atan(V_radar .* (t_eta_2d - eta_c(k) .* ones(Na,Nr)) / obj_list(obj_num(k),1));
wa = (sinc(theta_wa ./ wave_width)) .^ 2;
echo = echo + obj_list(obj_num(k),3) .* wr .* wa .* exp(-j * 4 * pi / lamda .* Rn) .* exp(j * pi * Kr .* (tau_2d - 2 .* Rn ./ c) .^ 2);
end
|
其中echo数组存储了雷达的回波数据
BP算法
在实际中,对回波信号的成像处理存在距离徙动这一问题,必须进行聚焦处理
这是因为雷达发射机发射的球面波,对回波进行距离压缩处理后,徙动轨迹是弯曲的
而BP成像算法有效地解决了这一问题,因为其具有精确到每个像素点的特点,不需要再散射点进行聚焦处理,以逐点成像的方式最后实现对目标区域的高分辨率成像
基本原理
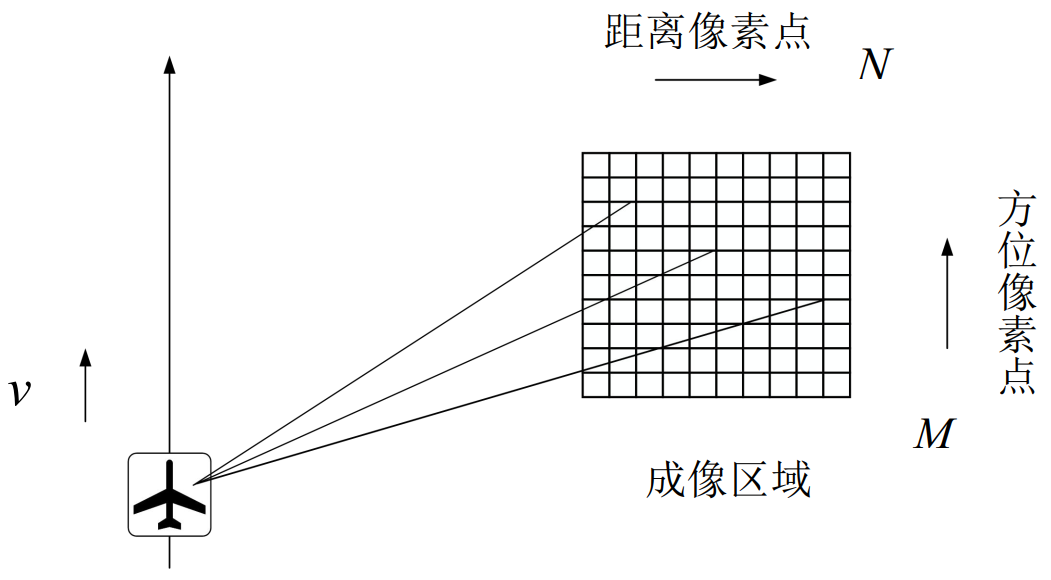
如图所示,图中将目标成像区域划分为M×N的网格,M为成像区域的方位向大小,N为成像区域的距离向大小,v为雷达载机的直线飞行速度
雷达接收机接收到目标反射回来的回波信号
在后续处理之前,先要对回波数据进行距离向的脉冲压缩,如下所示
sout(τ,u)=sr(τ,u)⨂P∗(−τ)
其中P∗(−τ)是P(τ)(反射的回波,未乘以反射系数)时间反转后的共轭,⨂为快时间卷积,u为雷达载机在X轴上的位置
然后计算雷达天线相位中心和目标成像区域各个网格点的斜距和时延
根据计算出来的斜距和时延,各个方位向下每个网格点都会得到一个回波数据
然后将各个方位向下所有网格点上的回波数据相干累加
累加完毕得到最终成像图像数据,具体如下所示
f(xm,yn)=∫usout[τmn(u),u]exp[j2πfcτmn(u)]du
其中,(xm,yn)为成像网格中第(m,n)个网格点,τmn(u)=c2xm2+(yn−u)2为雷达处于坐标(0,u)时,到成像网格点(xm,yn)的双程时延
算法流程
BP算法的运算过程主要包括以下几步:
- 对SAR回波数据进行脉冲压缩处理
- 根据成像需求,将目标成像区域划分为网格,获取所有像素点的坐标
- 计算当前方位向上,雷达天线相位中心与每个网格点的斜距和时延,然后根据计算出来的时延使得每个网格点都得到一个回波数据
- 对每个网格点上的回波数据进行相位补偿
- 重复第3,4步,直到遍历了所有的网格点和方位向各网格点数据沿着方位时刻相干叠加
- 数据累加完毕,得到成像数据
算法仿真
暂略,有时间再更
RD算法
CS算法







