参考的书籍是《深入浅出PyTorch——从模型到源码》，书中源代码仓库为https://github.com/zxjzxj9/PyTorchIntroduction

部分代码由于版本兼容性无法运行，文中会做出适当修改

学习路径

由于篇幅限制，我决定将源码学习分为多篇文章依次进行更新，以下为推荐的博客学习路径

  1. Pytorch学习（基础知识）
  2. Pytorch学习（运行逻辑）
  3. Pytorch高级应用

Pytorch底层逻辑

Pytorch中的模块简介

模块类

模块本身是一个类nn.Module，Pytorch的模型通过继承该类，在类的内部定义子模块的实例化，通过前向计算调用子模块，最后实现深度学习模型的搭建

下面给出继承nn.Module类的示例

1
2
3
4
5
6
7
8
9
10
11
import torch
import torch.nn as nn

class Model(nn.Module):
    def __init__(self, ...): # 定义类的初始化函数，...是用户的传入参数
        super(Model, self).__init__()
        ... # 根据传入的参数来定义子模块
    
    def forward(self, ...): # 定义前向计算的输入参数，...一般是张量或者其他的参数
        ret = ... # 根据传入的张量和子模块计算返回张量
        return ret

整个模块的函数主要由两部分构成：

  1. 通过__init__方法初始化整个学习模型
  2. 通过forward方法对该模型进行前向计算

在__init__方法的时候，可以在类的内部初始化子模块，然后在forward方法内调用这些子模块

初始化模型的时候需要使用super函数来获取当前类的父类（即nn.Module），然后调用父类的构造函数，从而初始化一些必要的变量

基于模块类的简单线性回归类

下面将利用模块类构造一个线性回归模型作为示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import torch
import torch.nn as nn

class LinearModel(nn.Module):
    def __init__(self, ndim):
        super(LinearModel, self).__init__()
        self.ndim = ndim

        self.weight = nn.Parameter(torch.randn(ndim, 1)) # 定义权重
        self.bias = nn.Parameter(torch.randn(1)) # 定义偏置

    def forward(self, x):
        # 定义线性模型 y = Wx + b
        return x.mm(self.weight) + self.bias

这个线性回归模型是输入一个特征的张量，做线性变换，输出一个预测张量

为了能够构造线性变换，我们需要知道输入特征维度的大小，并且知道线性回归的权重（self.weight）和偏置（self.bias）

在forward方法中，输入一个特征张量x\pmb x（大小为迷你批次大小×\times特征维度大小），做线性变换（使用mm方法做矩阵乘法），再加上偏置的值，最后输出一个预测值

需要注意的是模型的初始化部分，self.weight和self.bias是模型的参数，并且一开始就被初始化了，使得每个分量为标准正态分布（torch.randn）

此外，还需要使用nn.Parameter来包装这些参数，使之成为子模块（这些子模块中只包含参数），因为后续训练时需要对参数进行优化，只有把张量转换成参数才能在后续优化过程中被优化器访问到

下面给出调用LinearModel类的示例

1
2
3
4
lm = LinearModel(5)  # 定义线性回归模型，特征数为5
x = torch.randn(4, 5)  # 定义随机输入，迷你批次大小为4
print(x)
print(lm(x))  # 得到每个迷你批次的输出

输出为

1
2
3
4
5
6
7
8
tensor([[-1.0056, -0.9958, -0.1126,  1.7074, -0.3133],
        [-0.5071, -0.0030, -0.5264, -0.7031,  0.6047],
        [ 1.0955, -0.0601, -0.1676,  0.0738,  0.8772],
        [-1.1114, -0.5136,  0.2992,  0.9811, -0.9319]])
tensor([[3.4679],
        [0.4233],
        [1.8338],
        [0.7384]], grad_fn=<AddBackward0>)

线性回归类的实例化和方法调用

对于Pytorch的模块，有一些常用的方法可以在训练和预测时调用

  • 使用named_parameters方法和parameters方法获取模型的参数

通过调用named_parameters方法返回一个Python的生成器（Generator），通过访问生成器的对象得到的是该模型所有参数的名称和对应的张量值

通过调用parameters方法，Pytorch的优化器直接接受模型的参数生成器作为函数的参数，并且会根据梯度来优化生成器里的所有张量（该过程在反向传播时进行）

  • 使用train方法和eval方法进行模型训练和测试状态的转换

Pytorch模型的部分子模块（如dropout层和BatchNorm层）在训练时和测试时的状态是不同的，这就导致了模型必须在两种状态之间来回切换

调用train方法可以将模块（包括所有的子模块）转换到训练状态，调用eval方法可以将模块（包括所有的子模块）转换到预测状态

  • 使用`register_buffers方法设置缓存

除了通过反向传播得到梯度来进行训练的参数外，还有一些参数并不参与梯度传播，优化器并不会改变其值，只能由人为设置，称为缓存（Buffer）

通过调用register_buffer方法可以注册一个不需要梯度的张量，且可以出现在模型的state_dict()内部，例如BatchNorm里running_mean 和 running_var 就是通过 register_buffer 注册的

一些超参数就可以通过register_buffer进行设置

  • 使用named_children方法和children方法获取模型的子模块

有时需要对模块的子模块进行迭代，这时就需要使用named_children方法和children方法来获取子模块名字、子模块的生成器，以及只有子模块的生成器

由于PyTorch 模块的构造可以嵌套，所以子模块还有可能有自身的子模块，如果要获取模块内部所有模块的信息，可以使用named_modules和modules来得到相关信息

  • 使用apply方法递归地对子模块进行函数应用

如果需要对PyTorch所有的模块应用一个函数，可以使用apply方法，通过传入一个函数或者匿名函数来递归地应用这些函数，传入的函数以模块作为参数，在函数内部对模块进行修改

  • 改变模块参数数据类型和存储的位置

除对模块进行修改外，在深度学习模型的构建中还可能对参数进行修改

和张量的运算一样，可以改变模块的参数所在的设备（CPU或者GPU），具体可以通过调用模块自带的cpu方法和cuda方法来实现

另外，如果需要改变参数的数据类型，可以通过调用to方法加上需要转变的目标数据类型来实现

1
2
3
4
5
6
7
8
9
10
11
lm = LinearModel(5) # 定义线性模型
x = torch.randn(4, 5) # 定义模型输入
print(lm(x)) # 根据模型获取输入对应的输出
lm.named_parameters() # 获取模型参数（带名字）的生成器
print(list(lm.named_parameters())) # 转换生成器为列表
lm.parameters() # 获取模型参数（不带名字）的生成器
print(list(lm.parameters())) # 转换生成器为列表
lm.cuda() # 将模型参数移到GPU上
print(list(lm.parameters())) # 显示模型参数，可以看到已经移到了GPU上（device='cuda:0'）
lm.half() # 转换模型参数为半精度浮点数
print(list(lm.parameters())) # 显示模型参数，可以看到已经转换为了半精度浮点数（dtype=torch.float16）

输出为

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
tensor([[-4.6322],
        [ 4.5306],
        [-5.0074],
        [ 1.3283]], grad_fn=<AddBackward0>)
[('weight', Parameter containing:
tensor([[-0.9382],
        [ 0.7993],
        [ 1.9369],
        [-0.7825],
        [ 1.4315]], requires_grad=True)), ('bias', Parameter containing:
tensor([-1.1508], requires_grad=True))]
[Parameter containing:
tensor([[-0.9382],
        [ 0.7993],
        [ 1.9369],
        [-0.7825],
        [ 1.4315]], requires_grad=True), Parameter containing:
tensor([-1.1508], requires_grad=True)]
[Parameter containing:
tensor([[-0.9382],
        [ 0.7993],
        [ 1.9369],
        [-0.7825],
        [ 1.4315]], device='cuda:0', requires_grad=True), Parameter containing:
tensor([-1.1508], device='cuda:0', requires_grad=True)]
[Parameter containing:
tensor([[-0.9380],
        [ 0.7993],
        [ 1.9365],
        [-0.7827],
        [ 1.4316]], device='cuda:0', dtype=torch.float16, requires_grad=True), Parameter containing:
tensor([-1.1504], device='cuda:0', dtype=torch.float16, requires_grad=True)]

Pytorch的计算图和自动求导机制

计算图的介绍

计算图一般分为静态图和动态图

静态图，顾名思义就是图是确定的，即整个运算过程预先定义好了，然后再次运行的过程中只运算而不再搭建计算图，看起来就是数据在规定的图中流动

动态图，就是计算图是动态生成的，即边运算边生成计算图，是一个不断完成的过程，可能每运行一行代码都会拓展计算图

动态图便于调试、灵活，静态图速度要高效一些，但是不能改变数据流向

计算图是静态的深度学习框架，比较典型的就是Tensorflow，其也是因为张量在预先定义的图中流动而得名Tensorflow

Pytorch的计算图就是动态的，几乎每进行一次运算都会拓展原先的计算图，最后生成完成，进行反向传播，当反向传播完成，计算图默认会被清除，即进行前向传播时记录的计算过程会被释放掉

所以，默认情况下，进行一次前向传播后最多只能用生成的计算图进行一次反向传播

计算图的构建与启用

由于计算图的构建需要消耗内存和计算资源，在一些情况下，计算图并不是必要的，比如神经网络的推导

在这种情况下，可以使用torch.no_grad上下文管理器，在这个上下文管理器的作用域里进行的神经网络计算不会构建任何计算图

另外，还有一种情况是对于一个张量，我们在反向传播的时候可能不需要让梯度通过这个张量的节点，也就是新建的计算图要和原来的计算图分离

在这种情况下，可以使用张量的detach方法，通过调用这个方法，可以返回一个新的张量，该张量会成为一个新的计算图的叶子节点，新的计算图和老的计算图相互分离，互不影响，示例如下

1
2
3
4
5
6
7
8
9
10
import torch

t1 = torch.randn(3, 3, requires_grad=True)  # 初始化t1张量
t2 = t1.sum()
print(t2)  # t2的计算构建了计算图，输出结果带有grad_fn
with torch.no_grad():
    t3 = t1.sum()
print(t3)  # t3的计算没有构建计算图，输出结果没有grad_fn
print(t1.sum())  # 保持原来的计算图
print(t1.sum().detach())  # 和原来的计算图分离

输出为

1
2
3
4
tensor(-5.5670, grad_fn=<SumBackward0>)
tensor(-5.5670)
tensor(-5.5670, grad_fn=<SumBackward0>)
tensor(-5.5670)

自动求导机制

已知Pytorch会根据计算过程来自动生成动态图，然后可以根据动态图的创建过程进行反向传播，计算每个节点的梯度值

为了能够记录张量的梯度，在创建张量的时候需要设置一个参数require_grad=True，意味着这个张量会加入到计算图中，作为叶子节点参与计算

张量一旦指定了这个参数，在后续的计算中得到的中间结果的张量都会被设置成require_grad=True

对于Pytorch来说，每个张量都有一个grad_fn方法，这个方法包含着创建该张量的运算的导数信息，也包含着计算图的信息（该方法本身有一个next_functions属性，包含连接该张量的其他张量的grad_fn）

通过不断地反向传播回溯中间张量的计算节点，就可以得到所有张量的梯度，一个张量的梯度张量的信息保存在该张量的grad属性中

Pytorch的自动求导包

除PyTorch张量本身外，PyTorch提供了一个专门用来做自动求导的包，即torch.autograd，它包含有两个重要的函数，即torch.autograd.backward函数和torch.autograd.grad函数

torch.autograd.backward函数通过传入根节点张量，以及初
始梯度张量（形状和当前张量的相同），可以计算产生该根节点所有对应的叶子节点的梯度

当张量为标量张量时（Scala，即只有一个元素的张量），可以不传入初始梯度张量，默认会设置初始梯度张量为11

当计算梯度张量的时候，原先建立起来的计算图会被自动释放，如果需要再次做自动求导就会报错，因为之前的计算图已经不存在了，如果要在反向传播的时候保留计算图，可以设置retaingraph=True

另外，在自动求导的时候默认不会建立反向传播的计算图（因为反向传播也是一个计算过程，可以动态创建计算图），如果需要在反向传播计算的同时建立和梯度张量相关的计算图（在某些情况下，如需要计算高阶导数的情况下，不过这种情况比较少），可以设置creategraph=True

对于一个可求导的张量，也可以直接调用该张量内部的backward()方法来进行自动求导，示例如下

1
2
3
4
5
6
7
8
9
10
11
12
13
import torch

# 示例定义了一个函数f(x)=x^2，求导后为f'(x)=2x，用具体的张量来进行测试

t1 = torch.randn(3, 3, requires_grad=True)  # 定义一个3×3的张量
print(t1)
t2 = t1.pow(2).sum()  # 计算张量的所有分量平方和
t2.backward()  # 反向传播
print(t1.grad)  # 梯度是张量原始分量的2倍
t2 = t1.pow(2).sum()  # 再次计算所有分量的平方和
t2.backward()  # 再次反向传播
print(t1.grad)  # 梯度累积
print(t1.grad.zero_())  # 单个张量清零梯度的方法

输出为

1
2
3
4
5
6
7
8
9
10
11
12
tensor([[-0.2506, -0.0100, -0.4765],
        [-1.0155, -1.8206, -0.4870],
        [ 0.6104,  0.3032, -1.0589]], requires_grad=True)
tensor([[-0.5012, -0.0201, -0.9530],
        [-2.0309, -3.6412, -0.9740],
        [ 1.2208,  0.6064, -2.1178]])
tensor([[-1.0025, -0.0402, -1.9061],
        [-4.0618, -7.2825, -1.9481],
        [ 2.4417,  1.2128, -4.2356]])
tensor([[0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.]])

梯度函数的使用

PyTorch提供两种求梯度的方法：backward() 和torch.autograd.grad() ，他们的区别在于前者是给叶子节点填充.grad字段，而后者是直接返回梯度

下面举一个例子，设置一个计算图，其计算式为y=(x+1)×(x+2)y=(x+1)\times(x+2)，计算图如下所示

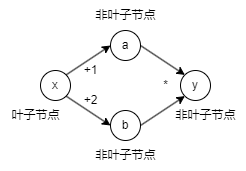
先使用backwward()进行梯度计算

1
2
3
4
5
6
7
8
9
10
import torch

x = torch.tensor(2., requires_grad=True)

a = torch.add(x, 1)
b = torch.add(x, 2)
y = torch.mul(a, b)

y.backward()
print(x.grad)

输出为

1
tensor(7.)

而对于autograd.grad()则为

1
2
3
4
5
6
7
8
9
10
import torch

x = torch.tensor(2., requires_grad=True)

a = torch.add(x, 1)
b = torch.add(x, 2)
y = torch.mul(a, b)

grad = torch.autograd.grad(outputs=y, inputs=x)
print(grad)

输出为

1
(tensor(7.),)

可以看到backward()方法是将计算好的梯度分别存储到各个张量的grad_fn属性内的，而torch.autograd.grad会直接返回一个存储梯度的元组

需要注意的一点是，张量绑定的梯度张量在不清空的情况下会逐渐累积，这种特性在某些情况下是有用的，比如需要一次性求很多迷你批次的累积梯度

但在一般情况下，不需要用到这个特性，所以要注意将张量的梯度清零

Pytorch的损失函数与优化器

损失函数

一般来说，PyTorch的损失函数有两种形式：函数形式和模块形式

前者调用的是torch.nn.functional库中的函数，通过传入神经网络预测值和目标值来计算损失函数，后者是torch.nn库里的模块，通过新建一个模块的实例，然后通过调用模块的方法来计算最终的损失函数

由于训练数据一般以迷你批次的形式输入神经网络，最后预测的值也是以迷你批次的形式输出的，而损失函数最后的输出结果应该是一个标量张量

因此，对于迷你批次的归约一般有两种方法，第一种是对迷你批次的损失函数求和，第二种是对迷你批次的损失函数求平均

一般来说，也是默认和最常见的情景，最后输出的损失函数是迷你批次损失函数的平均

此处以torch.nn.MSELoss模块作为示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import torch
import torch.nn as nn

mse = nn.MSELoss()  # 初始化平方损失函数模块
t1 = torch.randn(5, requires_grad=True)  # 随机生成张量t1
t2 = torch.randn(5, requires_grad=True)  # 随机生成张量t2
print(mse(t1, t2))  # 计算张量t1和t2之间的平方损失函数
t1 = torch.randn(5, requires_grad=True)  # 随机生成张量t1
t1s = torch.sigmoid(t1)
t2 = torch.randint(0, 2, (5,)).float()  # 随机生成0，1的整数序列，并转换为浮点数
bce = nn.BCELoss()  # 初始化二元交叉损失函数模块
print(bce(t1s, t2))  # 计算二分类的交叉熵
bce_logits = nn.BCEWithLogitsLoss()  # 使用交叉熵对数损失函数
print(bce_logits(t1, t2))  # 计算二分类的交叉熵，可以发现和前面的结果一致
N = 10  # 定义分类数目
t1 = torch.randn(5, N, requires_grad=True)  # 随机产生预测张量
t2 = torch.randint(0, N, (5,))  # 随机产生目标张量
t1s = torch.nn.functional.log_softmax(t1, -1)  # 计算预测张量的LogSoftmax
nll = nn.NLLLoss()  # 定义NLL损失函数
print(nll(t1s, t2))  # 计算损失函数
ce = nn.CrossEntropyLoss()  # 定义交叉熵损失函数
print(ce(t1, t2))  # 计算损失函数，可以发现和NLL损失函数的结果一致

输出为

1
2
3
4
5
tensor(2.7926, grad_fn=<MseLossBackward0>)
tensor(0.6353, grad_fn=<BinaryCrossEntropyBackward0>)
tensor(0.6353, grad_fn=<BinaryCrossEntropyWithLogitsBackward0>)
tensor(2.2134, grad_fn=<NllLossBackward0>)
tensor(2.2134, grad_fn=<NllLossBackward0>)

需要注意的是，torch.nn.BCELoss模块接收的是Sigmoid函数的输出，与之相比torch.nn.BCEWithLogitsLoss函数的区别是将Sigmoid函数的计算部分整合到了函数内部

当训练的时候若概率接近00或11的时候，二分类交叉熵函数的对数部分会很容易接近无穷大，会造成数值的不稳定，所以通过加入Sigmoid函数可以有效避免这种情况

和二分类的问题类似，在多分类情况下，也可以使用两个模块，第一个模块是torch.nn.NLLoss，即负对数似然函数

这个损失函数的运算过程是根据预测值（经过 Softmax的计算和对数计算）和目标值（使用独热编码）计算这两个值按照元素一一对应的乘积，然后对乘积求和，并取负值。因此，在使用这个损失函数之前必须先计算Sofmax函数取对数的结果，PyTorch中有一个函数torch.nn.functional.log_sofmax可以实现这个目的

第二个模块是torch.nn.CrossEntropyLoss，用于构建目标损失函数，这个损失函数可以避免LogSoftmax的计算,在损失函数里整合Softmax输出概率，以及对概率取对数输出损失函数

优化器

在有了损失函数之后，就可以使用优化器对模型进行优化了

此处示例数据是波士顿地区的房价，该数据有1313个特征，一共有506506条数据，采用SGD算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import torch
import torch.nn as nn
import pandas as pd
import numpy as np

data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
target = raw_df.values[1::2, 2]


class LinearModel(nn.Module):
    def __init__(self, ndim):
        super(LinearModel, self).__init__()
        self.ndim = ndim

        self.weight = nn.Parameter(torch.randn(ndim, 1))  # 定义权重
        self.bias = nn.Parameter(torch.randn(1))  # 定义偏置

    def forward(self, x):
        # 定义线性模型 y = Wx + b
        return x.mm(self.weight) + self.bias


lm = LinearModel(13)
criterion = nn.MSELoss()
optim = torch.optim.SGD(lm.parameters(), lr=1e-6)  # 定义优化器
data = torch.tensor(data, requires_grad=True, dtype=torch.float32)
target = torch.tensor(target, dtype=torch.float32)

for step in range(10000):
    predict = lm(data)  # 输出模型预测结果
    loss = criterion(predict, target)  # 输出损失函数
    if step and step % 1000 == 0:
        print("Loss: {:.3f}".format(loss.item()))
    optim.zero_grad()  # 清零梯度
    loss.backward()  # 反向传播
    optim.step()

输出为

1
2
3
4
5
6
7
8
9
Loss: 179.667
Loss: 155.831
Loss: 146.632
Loss: 139.157
Loss: 132.728
Loss: 127.168
Loss: 122.348
Loss: 118.159
Loss: 114.511

从代码中可以看到，首先要定义输入数据和预测目标，所以先构建有13个参数的线性回归模型LinearModel(13)，然后构建损失函数的计算模块criterion并设置为MSELoss模块的实例

之后构建了一个SGD优化器并传入相关的参数并进行优化，可以看到损失函数值在逐渐下降

在优化之前有两个步骤，第一步是调用zero_grad方法来清空所有的参数前一次反向传播的梯度，第二步是调用损失函数的backward方法来计算所有参数的当前的反向传播的梯度

除SGD之外，Pytorch还自带了许多其他的优化器，torch.optim包还提供了学习率衰减的相关类，这些类都在torch.optim.lr_scheduler中，可以使用torch.optim.lr_scheduler.StepLR类来进行学习率衰减

Pytorch中数据的输入与预处理

数据载入类

在训练模型的过程中，我们常常需要将原始数据转换成张量的格式以便于后续处理

一般而言，载入数据使用的是torch.utils.data.DataLoader类，为了能够使用DataLoader类，首先需要构建关于单个数据的torch.utils.data.Dataset类

映射类型的数据集

Dataset类有两种类型，其中一种是映射类型的，即对于数据集当中的每一个数据，都会有一个对应的索引，通过输入具体的索引，就能得到对应的数据，其构造方法如下所示

1
2
3
4
5
6
7
8
9
class Dataset(object):
    def __getitem__(self,index):
        #  index:数据索引(整数,范围为0至N-1)
        #  ...
        #  返回对应的数据张量
        
    def __len__(self):
        #  返回数据的总数
        #  ...

目前Dataset类已经取消了默认的__len__方法，因为可能会引发一些错误

而默认的方法现在为__getitem__和__add__ （用于拼接数据集）

所以可以得知对于这个类，主要需要重写两个方法

其中__getitem__方法输入整数数据索引，返回具体的某一条数据张量

__len__方法则返回数据的总数

可迭代类型的数据集

相比于映射类型的数据集，这个数据集不需要__getitem__和__len__方法，它本身更像是一个Python迭代器

不同于映射类型的数据集，其数据索引之间相互独立，在使用多进程载入数据的情况下，多个进程可以独立分配索引

在迭代器的使用过程中，因为索引之间存在前后顺序关系，需要考虑如何分割数据，使得不同的进程可以得到不同的数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class MyIterableDataset(torch.utils.data.IterableDataset):
     def __init__(self, start, end):
         super(MyIterableDataset).__init__()
         assert end > start, "this example code only works with end >= start"
         self.start = start
         self.end = end

     def __iter__(self):
         worker_info = torch.utils.data.get_worker_info()
         if worker_info is None:  # 单进程数据载入
             iter_start = self.start
             iter_end = self.end
         else:  # 多进程情况下需要分割数据
             per_worker = int(math.ceil((self.end - self.start) / float(worker_info.num_workers)))
             worker_id = worker_info.id
             iter_start = self.start + worker_id * per_worker
             iter_end = min(iter_start + per_worker, self.end)
         return iter(range(iter_start, iter_end))

根据不同的工作进程的序号设定不同进程数据迭代器的取值范围，从而保证不同的进程返回的数据各不相同

Pytorch模型的保存和加载

模块和张量的序列化及反序列化

由于PyTorch的模块和张量本质上是torch.nn.Module和torch.tensor类的实例，而PyTorch自带了一系列的方法，可以将这些类的实例转换成字符串，所以这些实例可以通过Python序列化方法进行序列化和反序列化

张量的序列化过程本质上是把张量的信息，包括数据类型和存储位置，以及携带的数据等转换为字符串，并进行存储

在Pytorch中，用于存储和载入模型的函数为torch.save和torch.load

在存储模型时，需要注意存储的模型数据是在CPU内还是在GPU内

在Pytorch中，一般模型有两种保存方式，第一种是直接保存模型的实例（因为模型本身也可以被序列化），第二种则是保存模型的状态字典，即一个包含模型所有参数的名字及其张量的字典

有了模型的状态字典后，可以通过load_state_dict方法传入该状态字典让模型载入参数