数据降维
数据降维算法
数据降维是针对高维度数据的数据预处理方法
简而言之,降维是将高维度的数据转换为低维度的数据,保留其最重要的一些特征且去除噪声和其他不重要的特征,从而提升数据处理的速度
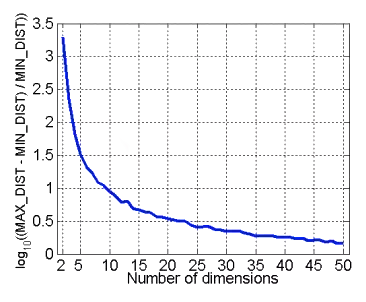
对于高维度的数据,有一个概念称为:维数灾难[1]
其描述的是在高维空间中的一些反直觉的现象,下面列出其中两点:
- 高维空间中的数据样本极其稀疏
- 高维单位空间当中的数据几乎全部位于超立方体的边缘
单位超立方体的体积为
而其内切的超球体的体积公式如下
对两者的商作极限可得
因此我们可以得出结论:一个高维的单元空间内只有边角,而没有中心数据也只能位于立方体的边缘上,而远离中心
由此我们可以推导出一个性质:在高维空间中,欧式距离失效(且任何基于欧氏距离的算法也都失效,例如K-means)
所以我们需要通过降维的方法来缓解维度灾难
降维有以下一些优点:
- 使高维度的数据更加容易使用
- 可以降低算法的计算开销
- 可以去除数据样本中的噪声及冗余成分
- 可以使处理结果更加直观和便于理解
主成分分析(PCA)
将坐标轴中心移到数据的中心,然后旋转坐标轴,使得数据在轴上的上的方差最大,即全部个数据个体在该方向上的投影最为分散,意味着更多的信息被保留下来,成为第一主成分
然后寻找第二主成分,使得与的协方差(相关系数)为,以免与信息重叠,并且使数据在该方向的方差尽量最大
以此类推,找到第三主成分,第四主成分第个主成分,个随机变量就有个主成分
摘自博客园[2]
PCA就是将数据投影到另一个坐标系(其维度一般小于等于原坐标系的维度)从而使得数据的方差最大
PCA的第一主成分即是能够使得原数据在此轴上方差最大的坐标轴,第二,三及其他主成分以此类推
PCA是一种线性变换,其本身不会改变点之间的距离
但是当我们开始删除维度时,距离就会被扭曲
也就是说,一些相隔很远的数据点可能在数据降维后变得很接近(尤其是当采用欧氏距离时)
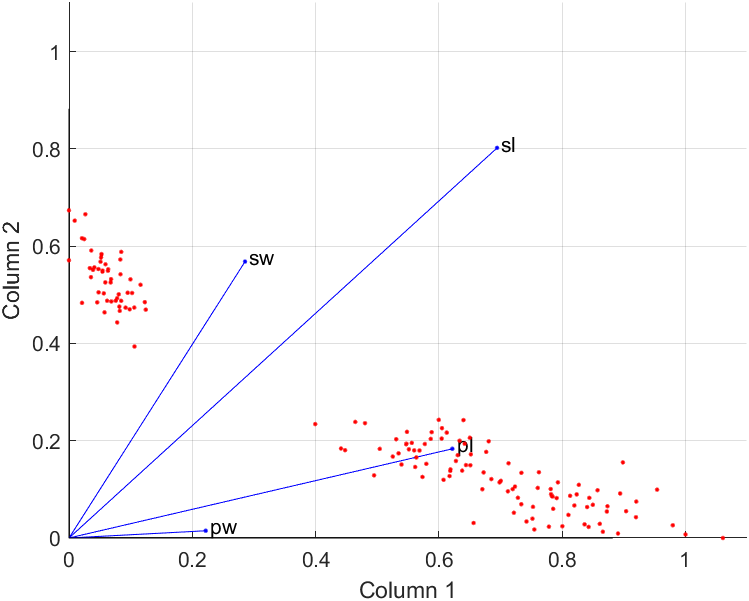
以下为MATLAB代码示例[3]
1 | load hald |
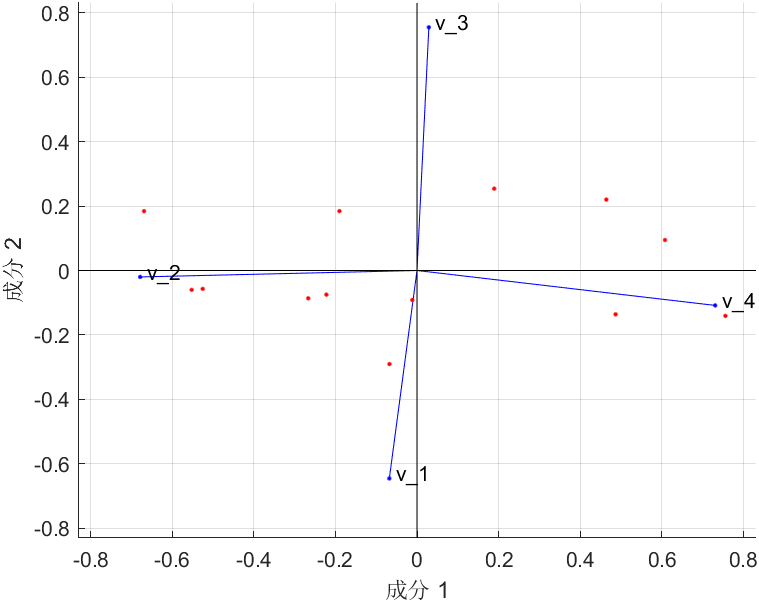
奇异值分解(SVD)
奇异值分解是矩阵分解的一种方式,我们定义矩阵的SVD分解如下所示
其中矩阵为对角矩阵,对角线上的元素即为奇异值,矩阵和都是酉矩阵[4],即满足
奇异值分解更详细的推导和步骤可以参考此篇博客,此处不做赘述
奇异值的性质
对于奇异值而言,它和我们熟悉的特征值分解很类似,在奇异值矩阵中,奇异值也是按照从大到小排列的
但是奇异值的减少是非常快的,在很多情况下,前甚至就占了全部奇异值之和的以上的比例
也就不难得出,我们可以通过最大的个奇异值和对应的左右奇异向量来近似描述原矩阵
应用
在PCA中,当样本量很大时,可以用SVD而非特征值分解来加速求解协方差矩阵最大的个特征向量张成的矩阵(即矩阵),在样本量很大的时候很有效
而奇异值对应的是PCA新坐标系中每个基对于整体数据的影响大小,可以通过提取奇异值最大的个基,来作为新的坐标
我们也可以使用SVD来压缩资料,比如图片,视频等,可以去除大部分不必要的细节,在保证不严重失真的情况下极大地减少存储所需的空间
SVD的缺点是分解出的矩阵解释性往往不强,类似于黑盒
线性判别算法(LDA)
不同于PCA方差最大化理论,LDA算法的思想是将数据投影到低维空间之后,使得同一类数据尽可能的紧凑,不同类的数据尽可能分散
因此,LDA算法是一种有监督的机器学习算法
同时,LDA有如下两个假设
- 原始数据根据样本均值进行分类
- 不同类的数据拥有相同的协方差矩阵
当然,在实际情况中,不可能满足以上两个假设
但是当数据主要是由均值来区分的时候,LDA一般都可以取得很好的效果
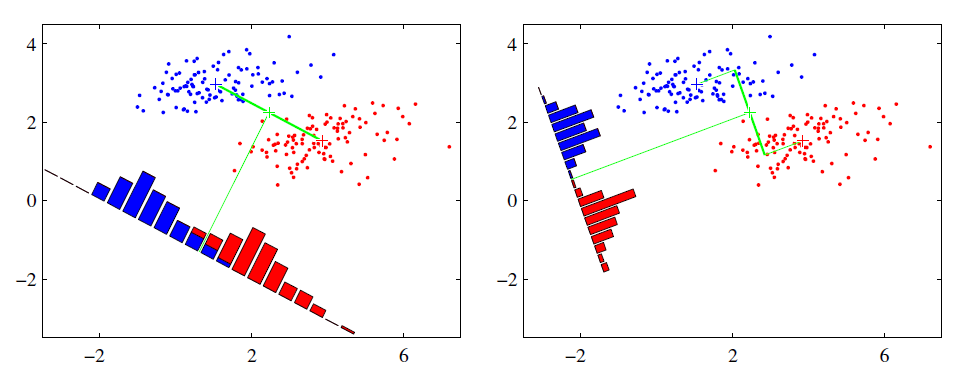
左边为PCA的结果,右边为LDA的结果
两种算法的相同点为:
- 均可以进行数据降维
- 降维时均采用了矩阵特征分解的思想
- 两者都假设数据符合高斯分布
不同点如下:
- LDA是有监督的降维,PCA是无监督的降维
- LDA最多降维到维,而PCA无限制
- LDA既可以用于降维,又可以用于分类
- LDA选择的是分类性能最好的投影方向,PCA会选择样本点投影具有最大方差的方向
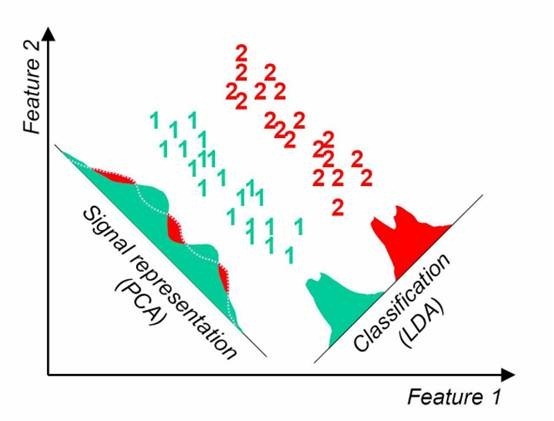
在这种条件下,明显LDA性能更优
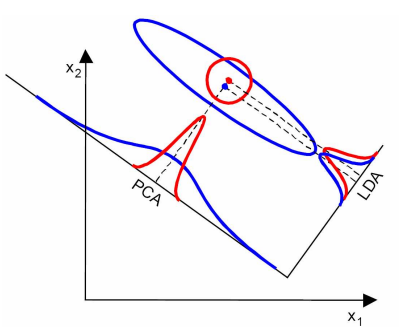
在另一种情况下,PCA的性能更佳
由此可见,在不同的条件下,两种算法其实各有优劣,需要根据实际情况选择
LDA的优点:
- 降维时可以使用类别的先验知识,而PCA无法使用
- LDA在依赖均值分类的问题中表现优于其他算法
缺点:
- LDA和PCA都不适合对非高斯样本进行降维
- LDA最多降维到维,不过也有一些LDA的改良算法可以绕过这个问题
- LDA在依赖方差分类的问题中表现较差
- LDA可能出现过拟合的情况
t 分布随机邻域嵌入(T-SNE)
流形学习
t-SNE(t 分布随机邻域嵌入)是一种无监督非线性降维技术,用于数据探索和可视化高维数据。非线性降维意味着该算法允许我们分离出无法用直线分离的数据
PCA(主成分分析)是一种线性技术,最适合具有线性结构的数据
它试图通过投影到较低维度、最小化方差并保留较大的成对距离来识别数据中的潜在主成分
但是,很多时候,高维数据并不是线性结构的,而是非线性结构的,例如下图所示

又或者是下面这种情况
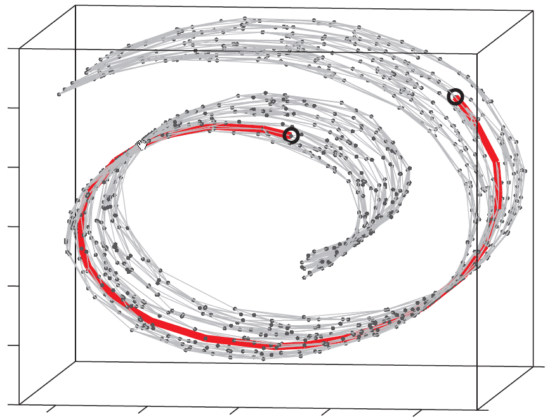
这时候很显然,PCA出来的结果效果肯定不理想,这时候就需要用到非线性降维技术
上图中就是一个很典型的流形学习的示例,也即是指我们观测到的数据维度是三维的,但是数据的本质是一个二维的流形
这就导致了图中所标注的两个点在流形上非常远,但从三维空间的欧氏距离来看,它们非常接近
所以说,流形学习的一个主要应用就是“非线性降维”,而t-SNE 是一种非线性降维技术,专注于保留低维空间中数据点之间的成对相似性
t-SNE 关注于保持较小的成对距离,能够保留低维空间中数据点之间的关系;而 PCA 则侧重于保持较大的成对距离以最大化方差
MATLAB实现分析
1 | load fisheriris |
我们这次仍然采用鸢尾花数据集进行分析
执行上述代码后,应该会输出t-SNE在二维和三维情况下的不同表现(即损失值),示例如下
2-D embedding has loss 0.1255, and 3-D embedding has loss 0.0980872.
1 | figure |
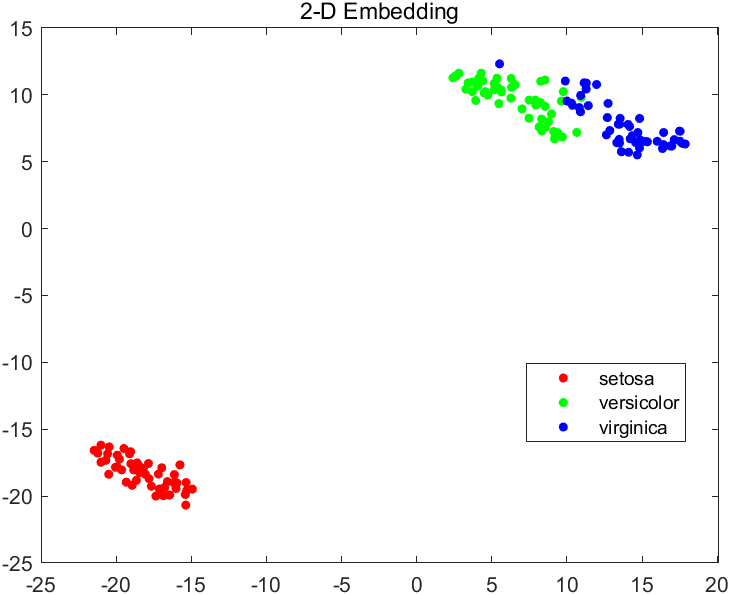
1 | figure |
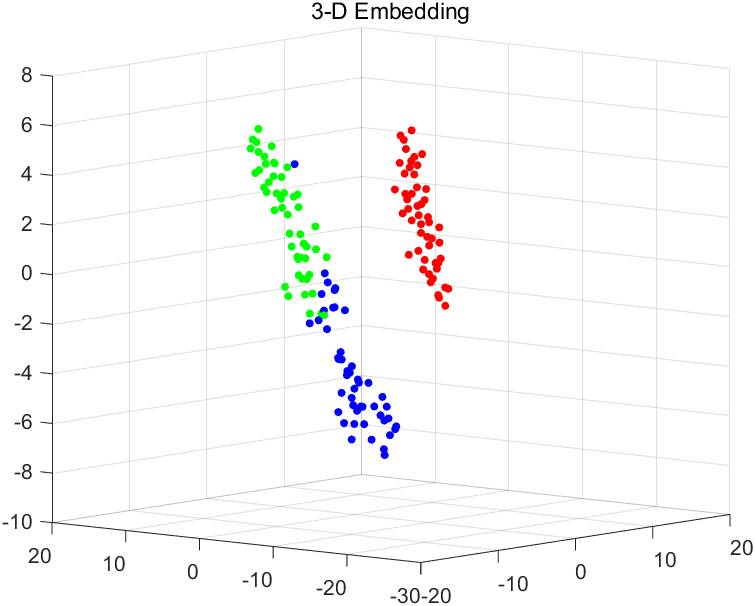
不难看出,在此数据集上,3D嵌入的损失更小,因为这种嵌入有更大的自由度来匹配原始数据
核主成分分析(KPCA)
简述
前面提到PCA并不适用于非线性的数据降维,所以,人们开发出了一种PCA的变体:即核主成分分析(Kernel PCA)
KPCA在PCA上只是多添加了一步:在进行降维之前,先通过一个非线性映射将输入的矩阵当中的所有样本映射到一个高维甚至是无穷维度的空间(称为特征空间),目的是使得映射后的数据线性可分,然后再进行PCA降维
KPCA的数学推导可以参见这篇博客,此处略去推导过程,得出结论
我们不需要显式地计算出矩阵映射到高维空间的映射,而只需得到高维空间的向量点积(即核函数)即可
核函数并不是随便定义的,通常指的是正定核
常用核函数
- 多项式核
更加一般化的形式为
- 高斯核
- Sigmoid核
非负矩阵分解(NMF)
非负矩阵分解顾名思义就是对于任意给定的一个非负矩阵,能够寻找到两个非负矩阵和,使得和的乘积可以合理近似矩阵,即
其损失函数主要关注Frobenius范数
1 | load fisheriris |